题目内容
已知数列{an}中,a1=5且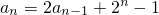 (n≥2且n∈N*).
(n≥2且n∈N*).
(1)若数列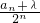 为等差数列,求实数λ的值;
为等差数列,求实数λ的值;
(2)求数列{an}的前n项和Sn.
解:(1)方法1:∵a1=5,
∴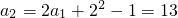 ,
,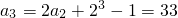 .
.
设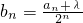 ,由{bn}为等差数列,则有2b2=b1+b3.
,由{bn}为等差数列,则有2b2=b1+b3.
∴ .
.
∴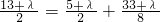 .
.
解得 λ=-1.
事实上,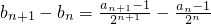 =
=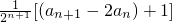 =
=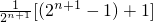 =1,
=1,
综上可知,当λ=-1时,数列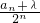 为首项是2、公差是1的等差数列.
为首项是2、公差是1的等差数列.
方法2:∵数列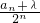 为等差数列,
为等差数列,
设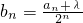 ,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*).
,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*).
∴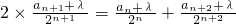 .
.
∴λ=4an+1-4an-an+2=2(an+1-2an)-(an+2-2an+1)=2(2n+1-1)-(2n+2-1)=-1.
综上可知,当λ=-1时,数列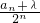 为首项是2、公差是1的等差数列.
为首项是2、公差是1的等差数列.
(2)由(1)知,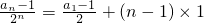 ,
,
∴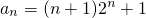 .
.
∴ .
.
即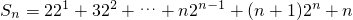 .
.
令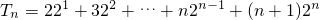 ,①
,①
则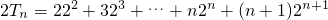 . ②
. ②
②-①,得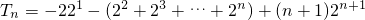 =n•2n+1.
=n•2n+1.
∴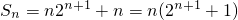 .
.
分析:(1)方法1:利用特殊到一般的方法,先探求实数λ的值,再验证一般性的结论成立;
方法2:设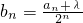 ,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*),由此可求实数λ的值;
,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*),由此可求实数λ的值;
(2)利用错位相减法,即可求数列{an}的前n项和Sn.
点评:本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力.
∴
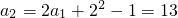 ,
,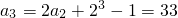 .
.设
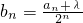 ,由{bn}为等差数列,则有2b2=b1+b3.
,由{bn}为等差数列,则有2b2=b1+b3.∴
 .
.∴
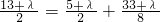 .
.解得 λ=-1.
事实上,
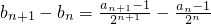 =
=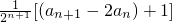 =
=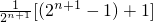 =1,
=1,综上可知,当λ=-1时,数列
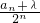 为首项是2、公差是1的等差数列.
为首项是2、公差是1的等差数列.方法2:∵数列
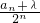 为等差数列,
为等差数列,设
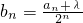 ,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*).
,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*).∴
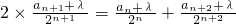 .
.∴λ=4an+1-4an-an+2=2(an+1-2an)-(an+2-2an+1)=2(2n+1-1)-(2n+2-1)=-1.
综上可知,当λ=-1时,数列
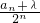 为首项是2、公差是1的等差数列.
为首项是2、公差是1的等差数列.(2)由(1)知,
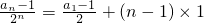 ,
,∴
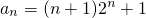 .
.∴
 .
.即
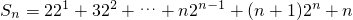 .
.令
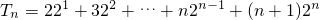 ,①
,①则
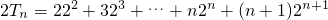 . ②
. ②②-①,得
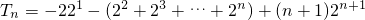 =n•2n+1.
=n•2n+1.∴
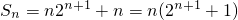 .
.分析:(1)方法1:利用特殊到一般的方法,先探求实数λ的值,再验证一般性的结论成立;
方法2:设
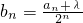 ,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*),由此可求实数λ的值;
,由{bn}为等差数列,则有2bn+1=bn+bn+2(n∈N*),由此可求实数λ的值;(2)利用错位相减法,即可求数列{an}的前n项和Sn.
点评:本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|