题目内容
(本小题满分13分)如图,在直四棱柱 中,底面是边长为
中,底面是边长为 的正方形,
的正方形, ,点E在棱
,点E在棱 上运动.
上运动.

(Ⅰ)证明: ;
;
(Ⅱ)若三棱锥 的体积为
的体积为 时,求异面直线
时,求异面直线 ,
, 所成的角.
所成的角.
(Ⅰ)详见解析; (Ⅱ) .
.
【解析】
试题分析:(Ⅰ)连接BD.要证 ,只要证
,只要证 平面
平面 ,可利用直棱柱的性质以及正方形ABCD来证明这一点.
,可利用直棱柱的性质以及正方形ABCD来证明这一点.
(Ⅱ)由四面体的体积为 ,可以求得
,可以求得 ,且可以证明
,且可以证明 就是异面直线
就是异面直线 ,
, 所成的角,于是可在直角三角形
所成的角,于是可在直角三角形 求出
求出 的大小.
的大小.
试题解析:【解析】
(Ⅰ)连接BD.
 是正方形,
是正方形, .
.
 四棱柱
四棱柱 是直棱柱,
是直棱柱,
 平面ABCD.
平面ABCD.
 平面ABCD,
平面ABCD,
 .
.
 平面
平面 .
.
 平面
平面 ,
,

 . (6分)
. (6分)
(Ⅱ) ,
, 平面
平面 ,
,
 .
.
 ,
, .
.
 .
.
 ,
, 为异面直线
为异面直线 ,
, 所成的角.
所成的角.
在
 中,求得
中,求得 .
.
 平面
平面 ,
, .
.
在
 中,求得
中,求得 ,
, .
.
所以,异面直线 ,
, 所成的角为
所成的角为 . (13分)
. (13分)
考点:1、空间直线与平面的位置关系;2、空间几何体的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中
,其中 为向量
为向量 与
与 的夹角,若
的夹角,若 ,
, ,
, ,则
,则 等于( )
等于( ) 为定义在R上的奇函数,且在
为定义在R上的奇函数,且在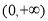 内是增函数,又
内是增函数,又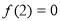 ,则不等式
,则不等式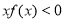 的解集为( )
的解集为( )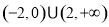

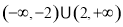
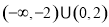
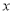 的方程
的方程 在区间[k-1,k+1]上有两个不相等的实根,则实数
在区间[k-1,k+1]上有两个不相等的实根,则实数 的取值范围是( )
的取值范围是( )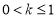 B.
B. C.
C.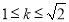 D.
D.
 的平均数是5,标准差是
的平均数是5,标准差是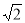 ,则
,则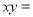 ( )
( )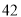 B.
B.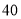 C.
C. D.
D.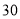
 为圆心,并且与直线
为圆心,并且与直线 相切的圆的方程为 .
相切的圆的方程为 . 在区间
在区间 上单调递增,且在这个区间上的最大值是
上单调递增,且在这个区间上的最大值是 ,那么
,那么
 B.
B. C.2 D.4
C.2 D.4 的直线
的直线 与双曲线
与双曲线 交于不同的两点P、Q,若点P、Q在
交于不同的两点P、Q,若点P、Q在 轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 .
轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 . 满足
满足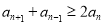 (
(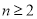 ),则称数列
),则称数列 的公差为
的公差为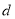 ,
,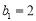 ,且数列
,且数列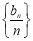 是凹数列,则
是凹数列,则