题目内容
【题目】已知双曲线
的右焦点为
， 
是双曲线C上的点， 
，连接
并延长
交双曲线C与点P，连接
，若
是以
为顶点的等腰直角三角形，则双曲线C的渐近线方程为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】如图，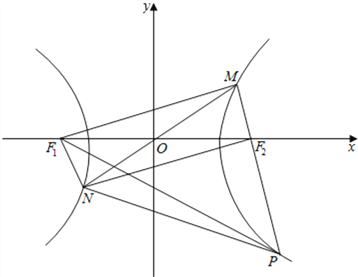
设F1为双曲线左焦点，连接MF1，NF1，则：
由对称性可知四边形F1NF2M
为平行四边形；
又△NF2P是以∠NF2P为顶角的等腰直角三角形，
可得∠MF2N=90°；
∴F1NF2M为矩形；
设|MF2|=x，由双曲线的定义可得，
|MF1|=2a+x；
∴|PF2|=|NF2|=|MF1|=2a+x；
∴|PF1|=2a+|PF2|=4a+x；
在Rt△MF1F2中有：
（2a+x）2+x2=4c2①；
在Rt△MF1P中有：（2a+x）2+（2a+2x）2=（4a+x）2②；
由②解得，x=a，代回①得：9a2+a2=4c2；
∴c2=
a2；∴b2=c2﹣a2=
a2； 
∴渐近线方程为：y=±
x=±
x．
故答案为：B．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
