题目内容
【题目】选修4-5:不等式选讲
已知函数![]() (其中
(其中![]() ).
).
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】试题分析:(1)方法一:分类讨论去掉绝对值,转化为一般的不等式,即可求解不等式的解集;
方法二:去掉绝对值,得到分段函数,画出函数的图象,结合图象即可求解不等式的解集.
(2)不等式![]() 即关于
即关于![]() 的不等式
的不等式![]() 恒成立,利用绝对值不等式,得
恒成立,利用绝对值不等式,得![]() ,进而求解实数
,进而求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当![]() 时,函数
时,函数![]() ,
,
则不等式为![]() ,
,
①当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() ;
;
②当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() .此时不等式无解;
.此时不等式无解;
③当![]() 时,原不等式为
时,原不等式为![]() ,解得:
,解得: ![]() ,
,
原不等式的解集为![]() .
.
方法二:当![]() 时,函数
时,函数![]()
 ,画出函数
,画出函数![]() 的图象,如图:
的图象,如图:
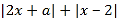
结合图象可得原不等式的解集为![]() .
.
(2)不等式![]() 即为
即为![]()
![]() ,
,
即关于![]() 的不等式
的不等式![]() 恒成立.
恒成立.
而![]()
![]()
![]()
![]() ,
,
所以![]() ,
,
解得![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目