题目内容
如图,在棱长为1的正方体ABCD—A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角的余弦值为( )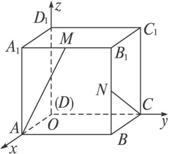
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
分析:可用基向量或建立空间直角坐标系用坐标法来求解.
解析:方法一:∵![]() ,
,
∴![]() .
.
而|![]() |=
|=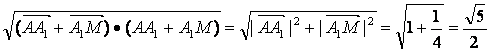 ,
,
同理,|![]() .
.
设直线AM与CN所成的角为α,则cosα= .
.
方法二:如图,把D点视作原点O,分别沿DA、DC、DD1方向为x轴、y轴、z轴的正方向建立空间直角坐标系.

则A(1,0,0),M(1,12,1),C(0,1,0),N(1,1,12).
∴![]() =(1,
=(1,![]() ,1)-(1,0,0)=(0,
,1)-(1,0,0)=(0,![]() ,1),
,1),
![]() =(1,1,
=(1,1,![]() )-(0,1,0)=(1,0,
)-(0,1,0)=(1,0,![]() ).
).
故![]() ·
·![]() =0×1+
=0×1+![]() ×0+1×
×0+1×![]() =
=![]() .
.
|![]() |=
|=![]() ,|
,|![]() |=
|=![]() .
.
设直线AM与CN所成的角为α,则
cosα= .
.
答案:D
点拨:空间两条直线之间的夹角是不超过90°的角,因此,如果按公式计算分子的数量积为一个负数,则应当取其绝对值,使之变为正值,这样求得的角为锐角,这一说明在以后很多计算问题中经常被用到.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
