Question

如图,在直三棱柱ABC—A₁B₁C₁中,AC=BC=CC₁=2,AC⊥BC,点D是AB的中点.

(1)求证:AC₁∥平面CDB₁;

(2)求点B到平面CDB₁的距离;

(3)求二面角BB₁CD的大小.

Answer 1

解法一：(1)证明:连结BC₁,设BC₁与B₁C的交点为E,连结DE.

∵D是AB的中点,E是BC₁的中点,∴DE∥AC₁.

∵DE平面CDB₁,AC₁平面CDB₁,∴AC₁∥平面CDB₁.

(2)设点B到平面CDB₁的距离为h.在三棱锥B₁—BCD中,

∵=,且B₁B⊥平面BCD,∴S_△BCD·B₁B=·h.

易求得S_△BCD=1,=CD·B₁D=,∴h=,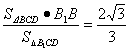

即点B到平面CDB₁的距离是.

(3)在平面ABC内作DF⊥BC于点F,过点F作FG⊥B₁C于点G,连结DG.

易证明DF⊥平面BCC₁B₁,从而GF是DG在平面BCC₁B₁内的射影,

根据三垂线定理得B₁C⊥GD.

∴∠DGF是二面角BB₁CD的平面角.

易求得DF=AC=1,GF=BE=.

在Rt△DFG中,∵tan∠DGF=,

∴二面角BB₁CD的大小是arctan.

解法二:∵在直三棱柱ABC—A₁B₁C₁中,AC=BC=CC₁=2,AC⊥BC,

∴AC、BC、CC₁两两垂直.

如图,以C为原点,直线CA、CB、CC₁分别为x轴、y轴、z轴,建立空间直角坐标系,

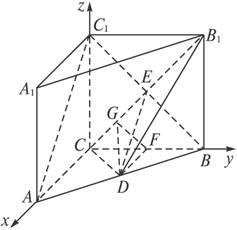
则C(0,0,0),A(2,0,0),B(0,2,0),C₁(0,0,2),D(1,1,0).

(1)证明:设BC₁与B₁C的交点为E,则E(0,1,1).

∵=(-1,0,1),=(-2,0,2),

∴=AC₁.

∴DE∥AC₁.

∵DE平面CDB₁,AC₁平面CDB₁,

∴AC₁∥平面CDB₁.

(2)设点B到平面CDB₁的距离为h.

在三棱锥B₁—BCD中,

∵,且B₁B⊥平面BCD,

∴S_△BCD·B₁B=·h.

易求得S_△BCD=1,=CD·B₁D=,

∴h=,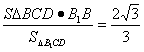

即点B到平面CDB₁的距离是.

(3)在平面ABC内作DF⊥BC于点F,过点F作FG⊥B₁C于点G,连结DG.

易证明DF⊥平面BCC₁B₁,从而GF是DG在平面BCC₁B₁内的射影,

根据三垂线定理得B₁C⊥GD.

∴∠DGF是二面角BB₁CD的平面角.

易知F(0,1,0),G(0,,),

∵=(0,,),=(1,,),

∴cos〈,〉==.

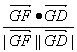∴二面角B-B₁C-D的大小是arccos.