题目内容
 为椭圆
为椭圆 上任意一点,
上任意一点,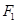 、
、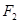 为左右焦点.如图所示:
为左右焦点.如图所示:

(1)若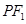 的中点为
的中点为 ,求证
,求证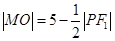 ;
;
(2)若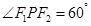 ,求
,求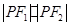 的值.
的值.
【答案】
(1))证明:在 中,
中, 为中位线
为中位线

(2)
【解析】
试题分析:(1)由椭圆定义知 ,则
,则 ,由条件知点
,由条件知点 、
、 分别是
分别是 、
、 的中点,所以
的中点,所以 为
为 的中位线,则
的中位线,则 ,从而命题得证;(2)根据椭圆定义,在
,从而命题得证;(2)根据椭圆定义,在 中有
中有 ,
, ,又由条件
,又由条件 ,从这些信息中可得到提示,应从余弦定理入手,考虑到
,从这些信息中可得到提示,应从余弦定理入手,考虑到 ,所以需将
,所以需将 两边平方,得
两边平方,得 ,将其代入余弦定理,得到关于
,将其代入余弦定理,得到关于 的方程,从而可得解.
的方程,从而可得解.
试题解析:(1)证明:在 中,
中, 为中位线
为中位线
 5分
5分
(2) ,
,
在 中,
中,
 ,
,
 12分
12分
考点:1.椭圆定义;2.余弦定理.

练习册系列答案
相关题目
 已知圆
已知圆