题目内容
(本小题满分12分)设函数 .
.
(1)若函数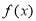 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数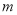 的取值范围;
的取值范围;
(2)若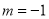 ,试比较当
,试比较当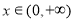 时,
时,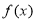 与
与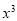 的大小;
的大小;
(3)证明:对任意的正整数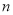 ,不等式
,不等式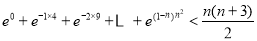 成立.
成立.
(1) ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)若可导函数 在指定的区间
在指定的区间 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为 (或
(或 恒成立,从而构建不等式,要注意“=”是否可以取到;(2)对于恒成立的问题,常用到两个结论:(1)
恒成立,从而构建不等式,要注意“=”是否可以取到;(2)对于恒成立的问题,常用到两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立 ;(3)数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题,用数学归纳法证明等式问题,要“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始值
;(3)数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题,用数学归纳法证明等式问题,要“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始值 是多少,由
是多少,由 时等式成立,推出
时等式成立,推出 时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
试题解析:(1)∵ 又函数
又函数 在定义域上是单调函数.
在定义域上是单调函数.
∴  或
或 在
在 上恒成立
上恒成立
若 在
在 上恒成立,即函数
上恒成立,即函数 是定义域上的单调地增函数,则
是定义域上的单调地增函数,则 在
在 上恒成立,由此可得
上恒成立,由此可得 ;
;
若 在
在 上恒成立,则
上恒成立,则 在
在 上恒成立.即
上恒成立.即 在
在 上恒成立.
上恒成立.
∵ 在
在 上没有最小值
上没有最小值
∴不存在实数 使
使 在
在 上恒成立.
上恒成立.
综上所述,实数 的取值范围是
的取值范围是 . 4分
. 4分
(2)当 时,函数
时,函数 .
.
令
则
显然,当 时,
时, ,
,
所以函数 在
在 上单调递减
上单调递减
又 ,所以,当
,所以,当 时,恒有
时,恒有 ,
,
即 恒成立.
恒成立.
故当 时,有
时,有 8分
8分
(3)数学归纳法
证明:1、当 时,左边=
时,左边= ,右边=
,右边= ,原不等式成立。
,原不等式成立。
2、设当 时,原不等式成立,
时,原不等式成立,
即
则当 时,
时,
左边=
只需证明
即证
即证
由(2)知
即
令 ,即有
,即有
所以当 时成立
时成立
由1、2知,原不等式成立
考点:1、函数单调性的应用;2、恒成立的问题;3、数学归纳法的应用.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

 (
( 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数 ( )
( ) B.
B. C.
C. D.
D.
 ,
, ,
, ,则集合
,则集合 等于( )
等于( ) B.
B. C.
C. D.
D.
 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线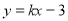 与平面区域
与平面区域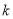 的取值范围为是
的取值范围为是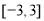

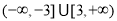

 的实部是
的实部是 B.
B. C.
C. D.
D.
 的首项为
的首项为 ,数列
,数列 为等比数列且
为等比数列且 ,若
,若 ,则
,则 .
. 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 的取值范围为是
的取值范围为是 B.
B.
 D.
D.
 存在垂直于
存在垂直于 轴的切线,且函数
轴的切线,且函数 在
在 上单调递减,则
上单调递减,则 的范围为 .
的范围为 . 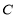 :
: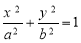 (
(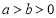 )过点(2,0),且椭圆C的离心率为
)过点(2,0),且椭圆C的离心率为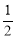 .
.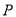 在直线
在直线 上,过
上,过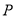 作直线交椭圆
作直线交椭圆 两点,且
两点,且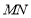 中点,再过
中点,再过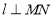 .求直线
.求直线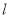 是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。