题目内容
 如图所示,巡逻艇在A处测得某走私船在东偏南45°方向距A处9海里的B处,正向南偏西15°方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(sin38°≈
如图所示,巡逻艇在A处测得某走私船在东偏南45°方向距A处9海里的B处,正向南偏西15°方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(sin38°≈5
| ||
| 14 |
分析:先设经过t小时在点C处刚好追上走私船,在△ABC中,求出|AB|,|AC|和|BC|,进而利用正弦定理求得sin∠BAC的值,再利用正弦定理可求得t.
解答: 解:设巡逻艇用t小时在C处追上走私船,作出如图的示意图.
解:设巡逻艇用t小时在C处追上走私船,作出如图的示意图.
依题意,在△ABC中,∠ABC=120°,|AB|=9,|AC|=28t,|BC|=20t
由正弦定理得:
=
⇒sinA=
又 sin38°≈
,所以 A≈38°…(6分)
∴sinC=sin(A+B)=sinAcosB+cosAsinB=
由
=
⇒t=
综上,巡逻艇应向东偏南38°,用45分钟就能追上走私船.…(14分)
 解:设巡逻艇用t小时在C处追上走私船,作出如图的示意图.
解:设巡逻艇用t小时在C处追上走私船,作出如图的示意图.依题意,在△ABC中,∠ABC=120°,|AB|=9,|AC|=28t,|BC|=20t
由正弦定理得:
| 28t |
| sin120° |
| 20t |
| sinA |
5
| ||
| 14 |
又 sin38°≈
5
| ||
| 14 |
∴sinC=sin(A+B)=sinAcosB+cosAsinB=
3
| ||
| 14 |
由
| 28t |
| sin120° |
| 9 |
| sinC |
| 3 |
| 4 |
综上,巡逻艇应向东偏南38°,用45分钟就能追上走私船.…(14分)
点评:本题主要考查了解三角形的实际应用.结合航海中的实际问题,与正弦定理知识有机结合,体现了数学在实际生活的应用过程.

练习册系列答案
相关题目
 如图所示,某巡逻艇在A处发现在北偏东45°,距A处8海里的B处有一走私船正沿南偏东75°的方向以12海里/小时的速度行驶,巡逻艇立即以12
如图所示,某巡逻艇在A处发现在北偏东45°,距A处8海里的B处有一走私船正沿南偏东75°的方向以12海里/小时的速度行驶,巡逻艇立即以12 方向距A处9海里的B处,正向南偏西
方向距A处9海里的B处,正向南偏西 方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(
方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(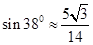 )
)
 如图所示,巡逻艇在A处测得某走私船在东偏南45°方向距A处9海里的B处,正向南偏西15°方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(
如图所示,巡逻艇在A处测得某走私船在东偏南45°方向距A处9海里的B处,正向南偏西15°方向行驶,速度为20海里/小时,如果巡逻艇以航速28海里/小时,则应在什么方向用多少时间才能追上这艘走私艇?(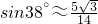 )
) )
)