题目内容
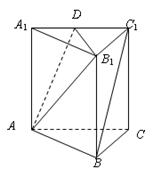
(本小题8分)如图所示,在正三棱柱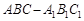 中,若
中,若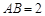 ,
,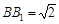 ,
,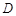 是
是 中点。
中点。
(1)证明: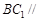 平面
平面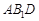 ;
;
(2)求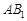 与
与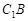 所成的角的大小。
所成的角的大小。
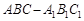 中,若
中,若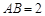 ,
,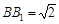 ,
,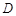 是
是 中点。
中点。
(1)证明:
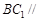 平面
平面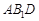 ;
;(2)求
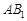 与
与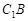 所成的角的大小。
所成的角的大小。(1)见解析;(2) 。
。
 。
。试题分析:(1)连接
 交
交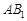 于点
于点 ,连接
,连接
正三棱柱
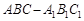 的侧面
的侧面 是矩形,所以
是矩形,所以 是
是 的中点
的中点又
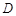 是
是 中点,所以
中点,所以 中
中 …………………… 2分
…………………… 2分 平面
平面 ,
, 平面
平面 ,所以
,所以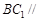 平面
平面 …………4分
…………4分(2)因为
 ,所以
,所以 (或其补角)等于
(或其补角)等于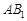 与
与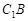 所成的角………………… 5分
所成的角………………… 5分计算得:
 ,所以
,所以 ,
, ……………7分
……………7分所以
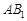 与
与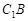 所成的角为
所成的角为 ………………8分
………………8分 (用向量法酌情给分)
点评:本题是一个典型的异面直线所成的角的问题,解答时也是应用典型的见中点找中点的方法,注意求角的三个环节,一画,二证,三求.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 m,
m, m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕 ,
, .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).

 的各棱长均为2,侧面
的各棱长均为2,侧面
 底面
底面 ,侧棱
,侧棱 与底面
与底面 .
. 与底面
与底面 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
 的边
的边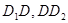 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使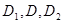 重合,记作D,给出下列位置关系:①SD
重合,记作D,给出下列位置关系:①SD 面EFD ; ②SE
面EFD ; ②SE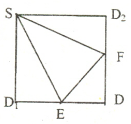
 ,其余棱长均为1,体积是
,其余棱长均为1,体积是 ,则函数
,则函数 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( ) 倍
倍 倍
倍 倍
倍 等于
等于




