题目内容
已知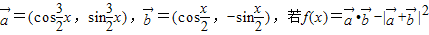 .
.(I)求函数f(x)的单调减区间;
(II)若x[-
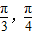 ],求函数f(x)的最大值和最小值.
],求函数f(x)的最大值和最小值.(文)已知
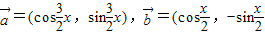 ),若f(x)=
),若f(x)=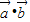
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若x∈[-
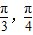 ],求函数f(x)的最大值和最小值.
],求函数f(x)的最大值和最小值.
【答案】分析:(理)(I)由题意可得:f(x)=
 -|
-| +
+ |2=
|2= •
• -2
-2 •
• =-
=- •
• -2=-cos2x-2,所以可得函数的单调减区间.
-2=-cos2x-2,所以可得函数的单调减区间.
(II)因为 ,所以
,所以 ,即
,即 ,进而得到函数的最值.
,进而得到函数的最值.
(文)(Ⅰ)由题意可得: =
= ,所以可得函数f(x)的最小正周期.(Ⅱ)∵
,所以可得函数f(x)的最小正周期.(Ⅱ)∵ ∴
∴ 所以
所以 ,即可得到函数的最值.
,即可得到函数的最值.
解答:(理)解:(I)因为 .
.
所以 ,
,
所以f(x)=
 -|
-| +
+ |2=
|2= •
• -2
-2 •
• =-
=- •
• -2
-2

所以函数 .
.
(II)因为 ,所以
,所以 ,即
,即 .
.
所以当 .
.
(文)解:(Ⅰ)因为 且
且
所以
= ,
,
∴函数f(x)的最小正周期为 .
.
(Ⅱ)∵
∴
所以 ,
,
因此,函数f(x)的最大值为1,最小值为 .
.
点评:解决此类问题的关键是熟练掌握向量的有关运算,以及三角函数的有关性质.

 -|
-| +
+ |2=
|2= •
• -2
-2 •
• =-
=- •
• -2=-cos2x-2,所以可得函数的单调减区间.
-2=-cos2x-2,所以可得函数的单调减区间.(II)因为
 ,所以
,所以 ,即
,即 ,进而得到函数的最值.
,进而得到函数的最值.(文)(Ⅰ)由题意可得:
 =
= ,所以可得函数f(x)的最小正周期.(Ⅱ)∵
,所以可得函数f(x)的最小正周期.(Ⅱ)∵ ∴
∴ 所以
所以 ,即可得到函数的最值.
,即可得到函数的最值.解答:(理)解:(I)因为
 .
.所以
 ,
,所以f(x)=

 -|
-| +
+ |2=
|2= •
• -2
-2 •
• =-
=- •
• -2
-2
所以函数
 .
.(II)因为
 ,所以
,所以 ,即
,即 .
.所以当
 .
.(文)解:(Ⅰ)因为
 且
且
所以

=
 ,
,∴函数f(x)的最小正周期为
 .
.(Ⅱ)∵

∴

所以
 ,
,因此,函数f(x)的最大值为1,最小值为
 .
.点评:解决此类问题的关键是熟练掌握向量的有关运算,以及三角函数的有关性质.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
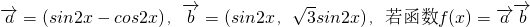 .
.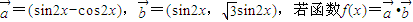 .
.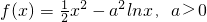 .
. .
. .
. .
.