题目内容
(本小题满分14分)
已知椭圆的中心在原点,焦点在 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点 (2,1),平行于
(2,1),平行于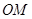 直线
直线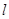 在
在 轴上的截距为
轴上的截距为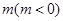 ,设直线
,设直线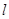 交椭圆于两个不同点
交椭圆于两个不同点 、
、 ,
,
(1)求椭圆方程;
(2)求证:对任意的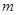 的允许值,
的允许值,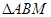 的内心在定直线
的内心在定直线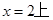 。
。
(1)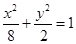 (2)直线
(2)直线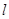 为
为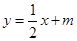 ,由
,由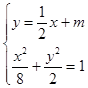 得
得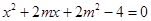 ,
,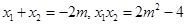 设直线
设直线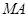 、
、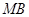 的斜率分别为
的斜率分别为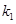 、
、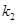 ,
,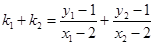
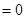 所以,
所以,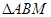 的角平分线垂直
的角平分线垂直 轴,因此,内心的横坐标等于点
轴,因此,内心的横坐标等于点 的横坐标,则对任意的
的横坐标,则对任意的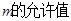 ,
,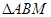 的内心在定直线
的内心在定直线 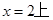
解析试题分析:(1)设椭圆方程为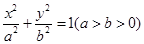
则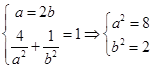 所以椭圆方程为
所以椭圆方程为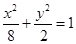 …… 5分
…… 5分
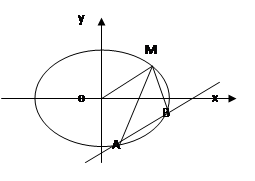
(2)如图,因为直线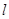 平行于
平行于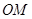 ,且在
,且在 轴上的截距为
轴上的截距为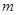 ,又
,又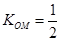 ,所以,直线
,所以,直线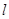 的方程为
的方程为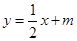 , 由
, 由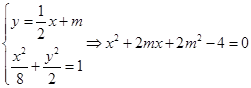 ,
,
设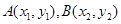 ,则
,则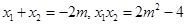 ,…………8分
,…………8分
设直线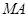 、
、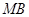 的斜率分别为
的斜率分别为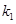 、
、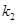 ,则
,则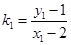 ,
,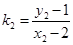
故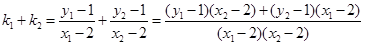 =
=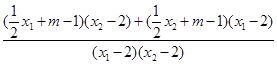 =
=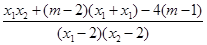
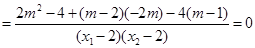 ……………12分
……………12分
故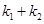 =0, 所以,
=0, 所以,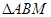 的角平分线垂直
的角平分线垂直 轴,因此,内心的横坐标等于点
轴,因此,内心的横坐标等于点 的横坐标,则对任意的
的横坐标,则对任意的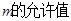 ,
,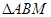 的内心在定直线
的内心在定直线 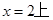 ……14
……14
考点:椭圆方程及直线与椭圆的位置关系
点评:直线与椭圆相交,利用韦达定理设而不求是常用的思路,本题要证内心在定直线上转化为两边关于该直线对称,进而与斜率联系起来

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
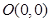 的距离是到定点
的距离是到定点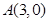 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.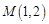 ,它们在
,它们在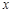 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.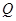 ,点
,点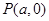 都满足
都满足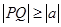 ,求
,求 的取值范围.
的取值范围.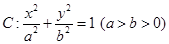 的一个焦点为
的一个焦点为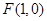 ,点
,点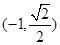 在椭圆
在椭圆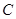 上,点
上,点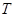 满足
满足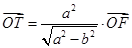 (其中
(其中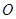 为坐标原点),过点
为坐标原点),过点 作一直线交椭圆于
作一直线交椭圆于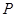 、
、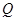 两点 .
两点 .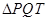 面积的最大值;
面积的最大值;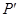 为点
为点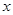 轴的对称点,判断
轴的对称点,判断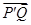 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.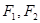 分别为椭圆
分别为椭圆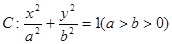 的左、右焦点,点
的左、右焦点,点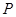 为椭圆上任意一点,
为椭圆上任意一点,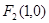 的距离的最大值为
的距离的最大值为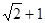 .
.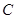 的方程。
的方程。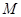 的坐标为
的坐标为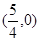 ,过点
,过点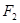 且斜率为
且斜率为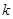 的直线
的直线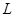 与椭圆
与椭圆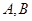 两点。对于任意的
两点。对于任意的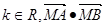 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。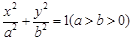 的离心率为
的离心率为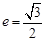 ,且过点(
,且过点(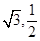 ),
),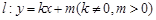 与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线的方程.
 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线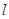 交
交 ,
, 两点:
两点: 的面积;
的面积; 是椭圆
是椭圆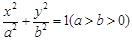 上一点,
上一点,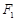 ,
,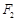 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足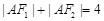
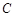 、
、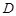 是椭圆上任两点,且直线
是椭圆上任两点,且直线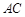 、
、 的斜率分别为
的斜率分别为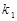 、
、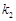 ,若存在常数
,若存在常数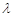 使
使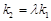 ,求直线
,求直线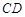 的斜率.
的斜率.