题目内容
定义在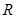 上的偶函数
上的偶函数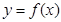 ,当
,当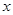 ≥0时,
≥0时,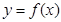 是单调递增的,
是单调递增的,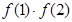 <0,则函数
<0,则函数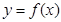 的图像与
的图像与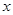 轴交点个数是 。
轴交点个数是 。
2。
解析试题分析:因为当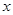 ≥0时,
≥0时,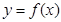 是单调递增的且
是单调递增的且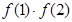 <0,所以
<0,所以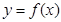 在
在 与x轴有且只有一个交点,又因为
与x轴有且只有一个交点,又因为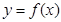 是偶函数,
是偶函数,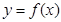 在
在 与x轴也有且只有一个交点,所以
与x轴也有且只有一个交点,所以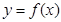 的图像与
的图像与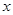 轴交点个数是2个。
轴交点个数是2个。
考点:本题考查函数的奇偶性和零点存在定理。
点评:函数的单调性与奇偶性的综合应用是一个难点,需要学生结合函数的图象充分理解好单调性和奇偶性这两个性质。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 恒成立,则k的取值范围为 。
恒成立,则k的取值范围为 。 满足
满足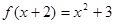 , 则
, 则 .
.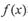 和,
和,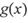 ,若对任意的
,若对任意的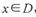 ,都有
,都有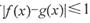 ,则称
,则称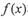 和
和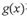 在D上是“密切函数”.给出定义域均为
在D上是“密切函数”.给出定义域均为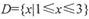 的四组函数:、
的四组函数:、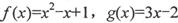

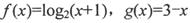
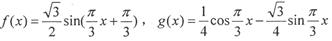
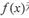 与
与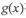 在D上为“密切函数”的是_______.
在D上为“密切函数”的是_______. ,那么
,那么 =_____________。
=_____________。 的定义域为 .
的定义域为 .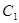 的方程是
的方程是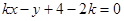
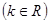 ,曲线
,曲线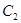 的方程是
的方程是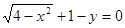 ,给出下列结论:
,给出下列结论: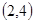 ;
;  ②曲线
②曲线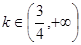 时,
时,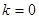 时,则
时,则 在
在 上具有单调性,则实数
上具有单调性,则实数 的取值范围是_______.
的取值范围是_______. 在
在 上为增函数,在
上为增函数,在 ____________;
____________;