Question

已知直线l₁:x-ky+k=0,l₂:kx-y-1=0,其中k为参数,求l₁,l₂交点的轨迹方程.

Answer 1

思路分析：

本题为求直线的交点轨迹方程问题,由直线方程的形式,既可以考虑参数方程来求解,又可以化为普通方程来求解,但在化为普通方程时需注意其等价性.

解法一：求出两直线的交点坐标,即解方程组.

当k²≠1时,得到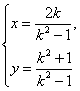（k为参数）.

这就是所求轨迹的参数方程,但如果要求轨迹的普通方程,需消去参数k.

解法二：由kx-y-1=0,

当x≠0时,可得k=,代入方程x-ky+k=0,得x-=0,去分母,化简得x²-y²+1=0(x≠0).

当x=0时,存在k=0,使得y=-1.

所以所求轨迹的普通方程为x²-y²+1=0(y≠1).

    方法归纳 (1)解法二中,方程两边同除以x,会丢x=0的解；方程两边同乘以x,会增x=0的根,所以最后得到轨迹方程后应检验是否是同解变形.

(2)两种方法得到轨迹的不同形式的方程,只要把参数方程中的参数消去,便可得到同样的普通方程.