题目内容
当α∈(0,
思路分析:这是一个超越不等式,直接利用代数方法很难得证,若在单位圆中作出正弦线、正切线及α弧段,借助几何图形建立面积不等式,则易证.
解:如右图,过A(1,0)作单位圆的切线,交α角终边于T,

则tanα=AT,
连结PA.
因为S△POA<S扇形OAP<S△OAT,
所以![]() ·|OA|·|MP|<
·|OA|·|MP|<![]() ·|OA|2·α<
·|OA|2·α<![]() ·|OA|·|AT|,
·|OA|·|AT|,
即![]() ·1·sinα<
·1·sinα<![]() ·12·α<
·12·α<![]() ·1·tanα,
·1·tanα,
从而sinα<α<tanα.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
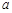 n}满足
n}满足 .
.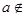 M;
M;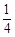 ]时,求证:
]时,求证: