题目内容
19.已知函数f(x)=2|x|+1.(1)作出其图象;
(2)由图象指出单调区间;
(3)由图象指出当x取何值时,函数有最值,求其最值,并写出值域.
分析 (1)将函数解析式化为分段函数的形式,再结合指数函数的图象,可得函数图象;
(2)由(1)中函数的图象可得单调区间;
(3)由(1)中函数的图象可得函数的最值和值域.
解答 解:(1)∵函数f(x)=2|x|+1=$\left\{\begin{array}{l}{2}^{-x}+1,x<0\\{2}^{x}+1,x≥0\end{array}\right.$,
故函数的图象如下图所示: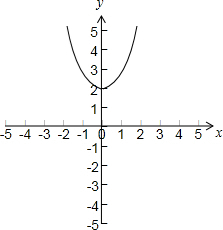
(2)由(1)中函数的图象可得:
函数f(x)=2|x|+1的单调递减区间为(-∞,0],
函数f(x)=2|x|+1的单调递增区间为[0,+∞),
(3)由(1)中函数的图象可得:
函数f(x)=2|x|+1在x=0时,取最小值2,无最大值,
故函数f(x)=2|x|+1的值域为[2+∞).
点评 本题考查的知识点是分段函数的应用,指数函数的图象和性质,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列命题中是真命题的是( )
| A. | 函数y=sin2x的最小正周期是2π | B. | 等差数列一定是单调数列 | ||
| C. | 直线y=ax+a过定点(-1,0) | D. | 在△ABC中,若sinB>0,则B为锐角 |
8.若loga-1(2x-1)>loga-1(x-1),则有( )
| A. | a>1,x>0 | B. | a>1,x>1 | C. | a>2,x>0 | D. | a>2,x>1 |