题目内容
已知函数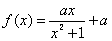 ,
,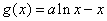 (
(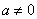 ).
).
(Ⅰ)求函数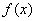 的单调区间;
的单调区间;
(Ⅱ)求证:当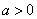 时,对于任意
时,对于任意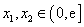 ,总有
,总有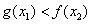 成立.
成立.
解:(Ⅰ)函数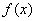 的定义域为
的定义域为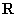 ,
,
 .
.
当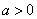 时,
时,
当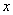 变化时,
变化时, ,
,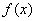 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| ↘ | ↗ | ↘ |
当 时,
时,
当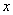 变化时,
变化时, ,
,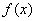 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| ↗ | ↘ | ↗ |
综上所述,
当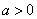 时,
时,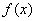 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ,
, ;
;
当 时,
时,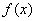 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 .
.
(Ⅱ)由(Ⅰ)可知,当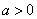 时,
时,
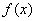 在
在 上单调递增,
上单调递增, ;
;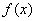 在
在 上单调递减,且
上单调递减,且 .
.
所以 时,
时,
 .
.
因为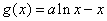 ,所以
,所以 ,
,
令 ,得
,得 .
.
①当 时,由
时,由 ,得
,得 ;由
;由 ,得
,得 ,
,
所以函数 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以 .
.
因为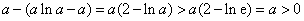 ,
,
所以对于任意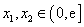 ,总有
,总有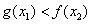 .
.
②当 时,
时, 在
在 上恒成立,
上恒成立,
所以函数 在
在 上单调递增,
上单调递增, .
.
所以对于任意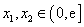 ,仍有
,仍有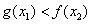 .
.
综上所述,对于任意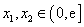 ,总有
,总有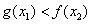 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 等于
等于 B.
B.  C.
C.  D.
D. 

 的不等式组
的不等式组 所构成的三角形区域内,则该质点到此三角形的三个顶点的距离均不小于
所构成的三角形区域内,则该质点到此三角形的三个顶点的距离均不小于 B.
B.  C.
C. D.
D.
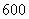 吨,每次都购买
吨,每次都购买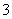 万元/次,
万元/次,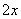 万元.若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.
万元.若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.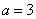 ,
,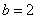 ,
,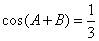 ,则
,则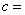 ( )
( )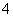
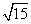
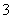
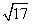
 满足
满足 ,
, ,则公差
,则公差 ______;
______; ______.
______.  .若关于
.若关于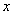 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是
的取值范围是 (B)
(B) (C)
(C) (D)
(D)
 都是正实数,且满足
都是正实数,且满足 ,则
,则 的最小值为
的最小值为