题目内容
已知角α的终边落在第一和第三象限的角平分线上,求α的六个三角函数值.
分析:当角α的终边落在第一象限的角平分线上时,在角α的终边上任意取一点A(1,1),再利用任意角的三角函数的定义求得α的六个三角函数值.当角α的终边落在第三象限的角平分线上时,同理求得α的六个三角函数值.
解答:解:当角α的终边落在第一象限的角平分线上时,在角α的终边上任意取一点A(1,1),
则 x=y=1,r=|OA|=
,
则由任意角的三角函数的定义可得 sinα=
=
=
,cosα=
=
=
,
tanα=
=1,cotα=
=1,secα=
=
,cscα=
=
.
当当角α的终边落在第三象限的角平分线上时,在角α的终边上任意取一点B(-1,-1),
则 x=y=-1,r=|OB|=
,
则由任意角的三角函数的定义可得 sinα=
=
=-
,cosα=
=
=-
,
tanα=
=1,cotα=
=1,secα=
=-
,cscα=
=-
.
则 x=y=1,r=|OA|=
| 2 |
则由任意角的三角函数的定义可得 sinα=
| y |
| r |
| 1 | ||
|
| ||
| 2 |
| x |
| r |
| 1 | ||
|
| ||
| 2 |
tanα=
| y |
| x |
| x |
| y |
| r |
| x |
| 2 |
| r |
| y |
| 2 |
当当角α的终边落在第三象限的角平分线上时,在角α的终边上任意取一点B(-1,-1),
则 x=y=-1,r=|OB|=
| 2 |
则由任意角的三角函数的定义可得 sinα=
| y |
| r |
| -1 | ||
|
| ||
| 2 |
| x |
| r |
| -1 | ||
|
| ||
| 2 |
tanα=
| y |
| x |
| x |
| y |
| r |
| x |
| 2 |
| r |
| y |
| 2 |
点评:本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中只有四个元素;
中只有四个元素; 在其定义域内为增函数;
在其定义域内为增函数; ,则角
,则角 的终边落在第四象限;
的终边落在第四象限; ,且点
,且点 不共线,已知
不共线,已知 ,则△
,则△ 是等腰三角形;
是等腰三角形;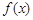 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 .
. 中只有四个元素;
中只有四个元素; ,则△ABC是等腰三角形;
,则△ABC是等腰三角形;