题目内容
已知复数ω满足ω2+ω+1=0,求值:ω2005= .
【答案】分析:由题意可得:ω=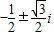 ,所以ω3=1.利用 2005=3×668+1,可得ω2005=(ω3)668ω=ω.
,所以ω3=1.利用 2005=3×668+1,可得ω2005=(ω3)668ω=ω.
解答:解:因为复数ω满足ω2+ω+1=0,
所以解得ω=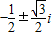 ,
,
所以ω3=1.
而 2005=3×668+1,
所以ω2005=(ω3)668ω=ω=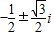 .
.
故答案为: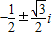 .
.
点评:本题是基础题,考查复数代数形式的有关,以及考查复数的基本概念.
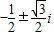 ,所以ω3=1.利用 2005=3×668+1,可得ω2005=(ω3)668ω=ω.
,所以ω3=1.利用 2005=3×668+1,可得ω2005=(ω3)668ω=ω.解答:解:因为复数ω满足ω2+ω+1=0,
所以解得ω=
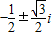 ,
,所以ω3=1.
而 2005=3×668+1,
所以ω2005=(ω3)668ω=ω=
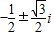 .
.故答案为:
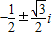 .
.点评:本题是基础题,考查复数代数形式的有关,以及考查复数的基本概念.

练习册系列答案
相关题目
 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 . 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 . 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 .