题目内容
函数f(x)=x(|x|-1)在[m,n]上的最小值为-
,最大值为2,则n-m的最大值为( )
| 1 |
| 4 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
| D、2 |
分析:根据二次函数的图象和性质,求出最大值和最小值对应的x的取值,然后利用数形结合即可得到结论.
解答:解:当x≥0时,f(x)=x(|x|-1)=x2-x=(x-
)-
≥-
,
当x<0时,f(x)=x(|x|-1)=-x2-x=(x+
)+
,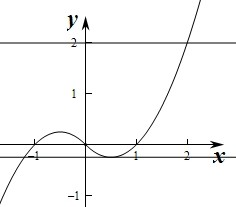
作出函数f(x)的图象如图:
当x≥0时,由f(x)=x2-x=2,解得x=2.
当x=
时,f(
)=-
.
当x<0时,由f(x)=)=-x2-x=-
.
即4x2+4x-1=0,解得x=
=
=
=
,
∴此时x=
,
∵[m,n]上的最小值为-
,最大值为2,
∴n=2,
≤m≤
,
∴n-m的最大值为2-
=
+
,
故选:B.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
当x<0时,f(x)=x(|x|-1)=-x2-x=(x+
| 1 |
| 2 |
| 1 |
| 4 |

作出函数f(x)的图象如图:
当x≥0时,由f(x)=x2-x=2,解得x=2.
当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
当x<0时,由f(x)=)=-x2-x=-
| 1 |
| 4 |
即4x2+4x-1=0,解得x=
-4±
| ||
| 2×4 |
-4±
| ||
| 8 |
-4±4
| ||
| 8 |
-1±
| ||
| 2 |
∴此时x=
-1-
| ||
| 2 |
∵[m,n]上的最小值为-
| 1 |
| 4 |
∴n=2,
-1-
| ||
| 2 |
| 1 |
| 2 |
∴n-m的最大值为2-
-1-
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
故选:B.
点评:本题主要考查函数最值的应用,利用二次函数的图象和性质是解决本题的关键,利用数形结合是解决本题的基本数学思想.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目