题目内容
请研究与函数f(x)=tanx相关的下列问题,在表中填写结论.
| 问 题 | 结 论(不需要过程) | 分数 | ||||||
求f(2x-
|
||||||||
求函数f(2x-
|
||||||||
写出f(2x-
|
||||||||
写出f(x-
|
||||||||
| 写出f(2x)图象的所有对称中心 |
分析:由f(x)=tanx,则f(2x-
)=tan(2x-
),然后利用复合函数的定义域,周期,单调性及值域的求解方法进行计算.
| π |
| 3 |
| π |
| 3 |
解答:解:
| 问 题 | 结 论 | ||||||||||
求f(2x-
|
{x|x∈R ,x≠
| ||||||||||
求函数f(2x-
|
周期为
| ||||||||||
写出f(2x-
|
增区间(
| ||||||||||
写出f(x-
|
(-∞,-1]∪[1,+∞) | ||||||||||
| 写出f(2x)图象的所有对称中心 | (
|
点评:本题考查了与正切函数有关的复合函数的定义域、值域、周期性与单调性的求法,解答的关键是熟记正切函数的有关性质,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (理)已知函数
(理)已知函数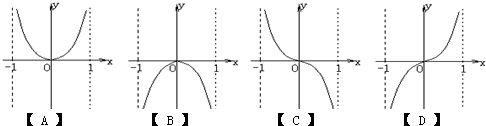

 (理)已知函数
(理)已知函数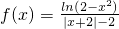 .
.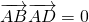 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
