题目内容
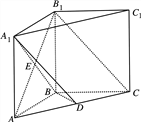
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析;(Ⅲ)点![]() 的轨迹是线段
的轨迹是线段![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ)求证:![]() 平面
平面![]() ,证明线面垂直,即证线线垂直,即在平面
,证明线面垂直,即证线线垂直,即在平面![]() 找两条相交直线与
找两条相交直线与![]() 垂直,由于底面
垂直,由于底面![]() 为菱形,则
为菱形,则![]() ,又
,又![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,即
,即![]()
![]() ,从而得证;(Ⅱ)求证:
,从而得证;(Ⅱ)求证:![]() ∥平面
∥平面![]() ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,注意到
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,注意到![]() 是
是![]() 的中点,连接
的中点,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,证得四边形
,证得四边形![]() 是平行四边形,从而得
是平行四边形,从而得![]() ∥
∥![]() ,从而可证
,从而可证![]() ∥平面
∥平面![]() ;(Ⅲ)连接
;(Ⅲ)连接![]() ,则
,则![]() ,又在
,又在![]() 中,
中,![]() ,又
,又![]() 为
为![]() 中点,所以
中点,所以![]()
![]()
![]() ,得
,得![]()
![]() 平面
平面![]() ,由已知可知,
,由已知可知,![]() ∥
∥![]() ,由
,由![]()
![]() ,得
,得![]() ,故
,故![]() 点一定在线段
点一定在线段![]() 上,这样就得到点
上,这样就得到点![]() 的轨迹,进而可得
的轨迹,进而可得![]() 的最小值.
的最小值.
试题解析:解:(Ⅰ)依题意, 因为四棱柱![]() 中,
中, ![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() .
.
又![]() 底面
底面![]() ,
,
所以![]()
![]() .
.
因为![]() 为菱形,
为菱形,
所以![]() .
.
而![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
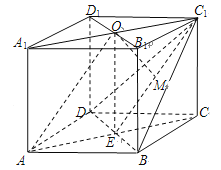
依题意, ![]() ∥
∥![]() ,
,
且![]() ,
, ![]() ,
,
所以![]() 为矩形.
为矩形.
所以![]() ∥
∥![]() .
.
又![]() ,
, ![]() ,
, ![]() ,
,
所以![]() =
= ![]() ,所以
,所以![]() 为平行四边形,
为平行四边形,
则![]() ∥
∥![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(Ⅲ)在![]() 内,满足
内,满足![]()
![]() 的点
的点![]() 的轨迹是线段
的轨迹是线段![]() ,包括端点.
,包括端点.
分析如下:连接![]() ,则
,则![]() .
.
由于![]() ∥
∥![]() ,故欲使
,故欲使![]()
![]() ,只需
,只需![]() ,从而需
,从而需![]() .
.
又在![]() 中,
中, ![]() ,又
,又![]() 为
为![]() 中点,所以
中点,所以![]()
![]()
![]() .
.
故![]() 点一定在线段
点一定在线段![]() 上.
上.
当![]() 时,
时, ![]() 取最小值.
取最小值.
在直角三角形![]() 中,
中, ![]() ,
, ![]() ,
,![]() ,
,
所以![]() .
.

练习册系列答案
相关题目