题目内容
【题目】平面内有向量 
=（1，7）， 
=（5，1）， 
=（2，1），点X为直线OP上的一个动点．
（1）当 
取最小值时，求 
的坐标；
（2）当点X满足（1）的条件和结论时，求cos∠AXB的值．
【答案】
（1）解：设 
=（x，y），
∵点X在直线OP上，∴向量 与 
共线．
又 =（2，1），∴x﹣2y=0，即x=2y．
∴ =（2y，y）．又 
= 
﹣ ， =（1，7），
∴ =（1﹣2y，7﹣y）．
同样 
= 
﹣ =（5﹣2y，1﹣y）．
于是 =（1﹣2y）（5﹣2y）+（7﹣y）（1﹣y）=5y2﹣20y+12=5（y﹣2）2﹣8．
∴当y=2时， 有最小值﹣8，此时 =（4，2）
（2）解：当 =（4，2），即y=2时，有 =（﹣3，5）， =（1，﹣1）．
∴| |= 
，| |= 
．
∴cos∠AXB=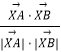 
=﹣ 
【解析】（1）因为点X在直线OP上，向量 与 共线，可以得到关于 坐标的一个关系式，再根据 的最小值，求得 的坐标，（2）cos∠AXB是 与 夹角的余弦，利用数量积的知识易解决．
练习册系列答案
阅读快车系列答案
相关题目
