题目内容
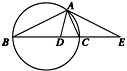
如图所示，设△ABC的外接圆的切线AE与BC的延长线交于点E，∠BAC的平分线与BC交于点D.求证：ED2=EC·EB.
证明略
解析:
证明 如图所示，因为AE是圆的切线，
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线，所以∠BAD=∠CAD.
从而∠ABC+∠BAD=∠CAE+∠CAD.
因为∠ADE=∠ABC+∠BAD，
∠DAE=∠CAE+∠CAD，
所以∠ADE=∠DAE，故EA=ED.
因为EA是圆的切线，所以由切割线定理知，
EA2=EC·EB，
而EA=ED，所以ED2=EC·EB.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
（2012•杭州二模）已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，在旋转过程中对应的俯视图的面积为S，则S的最大值为
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O、O′，现将此三棱柱绕直线OO′旋转（包括逆时针方向和顺时针方向），射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积记为S（x），则函数S（x）的最大值和最小正周期分别是（ ）