题目内容
下列计算错误的是
- A.∫-ππsinxdx=0
- B.∫01
 =
=
- C.
 cosxdx=2
cosxdx=2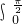 cosxdx
cosxdx - D.∫-ππsin2xdx=0
D
分析:利用微积分基本定理求出各选项的值,判断出D错.
解答:∫-ππsinxdx=(-cosx)|-ππ=(-cosπ)-(-cos(-π)=0

因为y=cosx为偶函数所以
 =π
=π
故选D
点评:本题考查利用微积分基本定理或定积分的几何意义求定积分值.
分析:利用微积分基本定理求出各选项的值,判断出D错.
解答:∫-ππsinxdx=(-cosx)|-ππ=(-cosπ)-(-cos(-π)=0

因为y=cosx为偶函数所以

 =π
=π故选D
点评:本题考查利用微积分基本定理或定积分的几何意义求定积分值.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
下列计算错误的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 B.
B. C.
C. D.
D.