题目内容
【题目】已知椭圆 ![]() (a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2
(a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的方程;
(2)是否存在同时满足①②两个条件的直线l?
①过点M(0, ![]() );
);
②存在椭圆上与右焦点F2共线的两点A、B,且A、B关于直线l对称.
【答案】
(1)解:∵椭圆 ![]() (a>0,b>0)上的点P到左、右两焦点F1,F2的距离之和为2
(a>0,b>0)上的点P到左、右两焦点F1,F2的距离之和为2 ![]() ,离心率为
,离心率为 ![]() ,
,
∴ 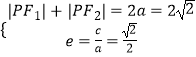 ,∴a=
,∴a= ![]() ,c=1,b=
,c=1,b= ![]() =1,
=1,
∴椭圆的标准方程为 ![]() =1.
=1.
(2)解:①假设存在符合条件的直线l,
当直线l与y轴重合时,两点A、B可位于长轴两个端点,符合条件.
此时l的方程为x=0;
②当直线l与x轴平行时,不符合条件;
③当直线l既不与x轴平行,又不与y轴重合时,
由F2(1,0),可设直线AB的方程为y=k(x﹣1),A(x1,y1),B(x2,y2),
则直线l的方程为y=﹣ ![]() ,
,
联立直线AB与椭圆方程 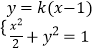 ,
,
化简得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
∴ ![]() ,
, ![]() ,
,
y1+y2=k(x1+x2)﹣2k= ![]() ,
,
∴AB的中点坐标为G( ![]() ,
, ![]() ).
).
结合题意知点G在直线l上,∴ ![]() =﹣
=﹣ ![]()
![]() +
+ ![]() ,
,
整理得:2k2﹣3k+1=0,解得k=1或k= ![]() ,
,
此时直线l的方程为y=﹣x+ ![]() 或y=﹣2x+
或y=﹣2x+ ![]() .
.
综上所述,存在符合条件的直线l,方程分别为x=0,y=﹣x+ ![]() 或y=﹣2x+
或y=﹣2x+ ![]()
【解析】(1)由椭圆定义和离心率,列出方程组,由此能求出椭圆的标准方程.(2)当直线l与y轴重合时,l的方程为x=0;当直线l与x轴行时,不符合条件; 当直线l既不与x轴平行,又不与y轴重合时,设直线AB的方程为y=k(x﹣1),直线l的方程为y=﹣ ![]() ,联立直线AB与椭圆方程,得(1+2k2)x2﹣4k2x+2k2﹣2=0,由此利用韦达定理、根的判别式能求出结果.
,联立直线AB与椭圆方程,得(1+2k2)x2﹣4k2x+2k2﹣2=0,由此利用韦达定理、根的判别式能求出结果.