题目内容
【题目】已知函数f(x)=loga ![]() ,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.
,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.
(1)求f(x)的定义域,并判断f(x)的奇偶性;
(2)已知区间D=[2a+1,2a+ ![]() ]满足3aD,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.
]满足3aD,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.
【答案】
(1)解:由 ![]() ,整理得(x+2a)(x﹣2a)>0,解得x<﹣2a,或x>2a,
,整理得(x+2a)(x﹣2a)>0,解得x<﹣2a,或x>2a,
∴f(x)的定义域为(﹣∞,﹣2a)∪(2a,+∞).
又∵ ![]() =
= ![]() ,
,
∴f(﹣x)=f(x),
∴f(x)为奇函数
(2)解:由已知3a[2a+1,2a+ ![]() ],
],
∴2a+1>3a,或2a+ ![]() <3a,即0<a<1,或a>
<3a,即0<a<1,或a> ![]() .
.
又∵要使g(x)有意义,就须使x+2a>0,且4a﹣x>0,即﹣2a<x<4a,
结合(1)中f(x)的定义域知函数h(x)的自变量x须满足2a<x<4a.
由题知h(x)在区间[2a+1,2a+ ![]() ]上有意义,
]上有意义,
∴ 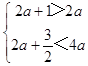 解得a>
解得a> ![]() ,
,
∴ ![]() <a<1,或a>
<a<1,或a> ![]() .
.
∵h(x)=f(x)+g(x)= ![]() +loga(x+2a)+loga(4a﹣x)=
+loga(x+2a)+loga(4a﹣x)= ![]() ,
,
∴|h(x)|≤2恒成立,即为| ![]() |≤2恒成立.
|≤2恒成立.
因为 3a[2a+1,2a+ ![]() ],所以h(x)≠2,
],所以h(x)≠2,
即题意转化为对任意x∈[2a+1,2a+ ![]() ],不等式﹣2≤
],不等式﹣2≤ ![]() 应恒成立.
应恒成立.
①当 ![]() 时,上式等价于a2<﹣x2+6ax﹣8a2≤a﹣2应恒成立.
时,上式等价于a2<﹣x2+6ax﹣8a2≤a﹣2应恒成立.
由于左端a2<﹣x2+6ax﹣8a2,即(x﹣3a)2<0,显然不成立.
②当 ![]() 时,问题转化为a﹣2≤﹣x2+6ax﹣8a2<a2应恒成立.
时,问题转化为a﹣2≤﹣x2+6ax﹣8a2<a2应恒成立.
对于右端﹣x2+6ax﹣8a2<a2,等价于(x﹣3a)2>0,显然成立.
研究左端 ![]() ≤0成立的条件.
≤0成立的条件.
令 ![]() ,对称轴x=3a,开口向上.
,对称轴x=3a,开口向上.
由 ![]() 知
知 ![]() ]上是减函数,
]上是减函数,
∴h(x)max=h(2a+1),
∴要使左端成立,只需h(2a+1)<0成立,
即需 ![]() ,
,
也就是需2a3﹣a2﹣1>0,
也就是(a﹣1)(2a2+a+1)>0,
只须a>1,而已知 ![]() ,故当
,故当 ![]() 时,不等式a﹣2≤﹣x2+6ax﹣8a2<a2恒成立.
时,不等式a﹣2≤﹣x2+6ax﹣8a2<a2恒成立.
综上所述,满足条件的a的取值范围为( ![]() ,+∞)
,+∞)
【解析】(1)由 ![]() ,解得:函数f(x)的定义域,再由函数奇偶性的定义,可判断出f(x)为奇函数.(2)若对任意x∈D,不等式|h(x)|≤2恒成立,即为|
,解得:函数f(x)的定义域,再由函数奇偶性的定义,可判断出f(x)为奇函数.(2)若对任意x∈D,不等式|h(x)|≤2恒成立,即为| ![]() |≤2恒成立,分类求出各种情况下满足条件的a值,综合可得实数a的取值范围.
|≤2恒成立,分类求出各种情况下满足条件的a值,综合可得实数a的取值范围.

【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ![]() ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(Ⅰ)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(Ⅱ)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2= ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |