题目内容
14.已知l:y=kx+b为曲线y=f(x)的“渐近线”,给出定义域均为D={x|x>1}的函数如下:①f(x)=$\sqrt{x}$;
②f(x)=$\frac{2x-3}{x}$;
③f(x)=$\frac{{x}^{2}+1}{x}$;
④f(x)=$\frac{xlnx+1}{lnx}$;
⑤f(x)=2(x-1-e-x).
其中,曲线y=f(x)存在“渐近线”的有(将序号填到横线上)②③④⑤.
分析 本题从大学数列极限定义的角度出发,构造渐近线函数,目的是考查学生分析问题、解决问题的能力,考生需要抓住本质:存在分渐近线的充要条件是x→∞时,y-f(x)→0进行作答.
解答 解:l:y=kx+b为曲线y=f(x)的“渐近线”的充要条件是x→∞时,y-f(x)→0.
对于①y=kx+b,f(x)=$\sqrt{x}$,当x>1时便不符合,所以①不存在;
对于②y=kx+b,f(x)=$\frac{2x-3}{x}$肯定存在渐近线,因为当时,y-f(x)→0;②正确.
对于③y=kx+b,k=0,b=0时,y是f(x)=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$的渐近线,③正确.
对于④y=kx+b,k=1,b=0,f(x)=$\frac{xlnx+1}{lnx}$=x+$\frac{1}{lnx}$,
所以当x→+∞时,y-f(x)会越来越小,趋近于0,
所以存在渐近线;④正确.
对于⑤y=kx+b,f(x)=2(x-1-e-x),k=2,b=-2时,
当x→∞时,y-f(x)=kx+b-2x+2+2e-x=2e-x→0,
因此存在渐近线.
故存在分渐近线的是:②③④⑤.
故答案为:②③④⑤.
点评 本题较难,涉及到部分大学内容,属于拓展类题目.是一道好题,思维灵活,要透过现象看本质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设m和n均为给定的大于1的自然数,集合M={0,1,2,…,m-1},A={x|x=x1+x2m+…+xnmn-1,xi∈M,i=1,2,…,n},设s,t∈A,s=a1+a2m+…+anmn-1,t=b1+b2m+…+bnmn-1,其中ai、bi∈M,i=1,2,…,n,则an<bn是s<t的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.“a=1“是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
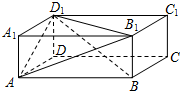 如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.
如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.