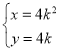题目内容
【题目】若函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅱ)若![]() ,方程
,方程![]() 至少有两个不等的解,求
至少有两个不等的解,求![]() 的取值集合;
的取值集合;
(Ⅲ)若函数![]() 为
为![]() 上的单调减函数,
上的单调减函数,
①求![]() 的取值范围;
的取值范围;
②若不等式![]() 成立,求实数
成立,求实数![]() 的取值集合.
的取值集合.
【答案】(Ⅰ)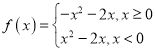 ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)①
;(Ⅲ)①![]() ,②
,②![]()
【解析】
首先根据函数的奇偶性求出函数解析式为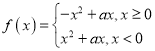 ,
,
(Ⅰ)将![]() 代入即可;(Ⅱ)将
代入即可;(Ⅱ)将![]() 代入求出此时函数解析式,画出函数图象,方程
代入求出此时函数解析式,画出函数图象,方程![]() 的解,转化为函数
的解,转化为函数![]() 与
与![]() 的交点,数形结合即可求解;(Ⅲ)将各段函数配成标准式,求出其对称轴,根据函数在定义域上单调递减求出参数
的交点,数形结合即可求解;(Ⅲ)将各段函数配成标准式,求出其对称轴,根据函数在定义域上单调递减求出参数![]() 的值,根据函数的奇偶性及单调性将函数不等式转化为自变量的不等式,最后解一元二次不等式即可;
的值,根据函数的奇偶性及单调性将函数不等式转化为自变量的不等式,最后解一元二次不等式即可;
解:因为函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() .
.
设![]() 则
则![]() ,
,![]()
因为![]()
所以![]() ,
,![]() ,
,
综上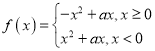
(Ⅰ)当![]() 时,
时,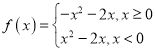 ;
;
(Ⅱ)当![]() 时,
时,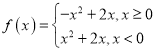 ,可画函数图象如下所示:
,可画函数图象如下所示:
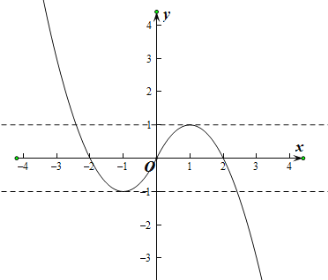
因为方程![]() 至少有两个不等的解,即函数
至少有两个不等的解,即函数![]() 与
与![]() 至少有两个交点,
至少有两个交点,
从函数图象可知![]()
即![]()
(Ⅲ)因为函数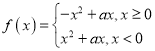 为
为![]() 上的单调减函数,
上的单调减函数,
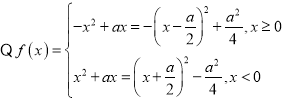
①当![]() 时,对称轴
时,对称轴![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 时,
时,![]() 在
在![]() 上为单调递减函数,
上为单调递减函数,
当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 上递减,不合题意,
上递减,不合题意,
所以函数![]() 为单调减函数时,
为单调减函数时,![]() 的范围为
的范围为![]() .
.
②![]() ,
,![]() ,
,
又![]() 是奇函数,
是奇函数,![]() ,
,
又因为![]() 为
为![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() ,
,
即![]() 解得
解得![]() 或
或![]()
即![]()

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】从某电子商务平台随机抽取了1000位网上购物者(年消费都达到2000元),并对他们的年龄进行了调查,统计情况如下表所示:
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 | 400 | 200 | 100 | 50 |
该电子商务平台将年龄在![]() 的人群定义为消费主力军,其它年龄段定义为消费潜力军.
的人群定义为消费主力军,其它年龄段定义为消费潜力军.
(1)若该电子商务平台共10万位网上购物者,试估计消费主力军的人数;
(2)为了鼓励消费潜力军消费,该平台决定对年消费达到2000元的购物者发放代金券,消费主力军每人发放100元,消费潜力军每人发放200元.现采用分层抽样(按消费主力军与消费潜力军分层)的方式从参与调查的1000位网上购物者中抽取10人,并在这10人中随机抽取3人进行回访,求这3人获得代金券总金额![]() (单位:元)的分布列及数学期望.
(单位:元)的分布列及数学期望.