题目内容
(本题满分14分) 已知数列 中的相邻两项
中的相邻两项 是关于
是关于 的方程
的方程 的两个根,且
的两个根,且 .
.
(Ⅰ)求 ,
, ,
, ,
, 及
及 (不必证明);
(不必证明);
(Ⅱ)求数列 的前
的前 项和
项和 .
.
 中的相邻两项
中的相邻两项 是关于
是关于 的方程
的方程 的两个根,且
的两个根,且 .
.(Ⅰ)求
 ,
, ,
, ,
, 及
及 (不必证明);
(不必证明);(Ⅱ)求数列
 的前
的前 项和
项和 .
.(I)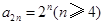 .
.
(II)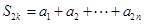
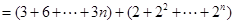
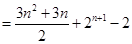
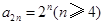 .
.(II)
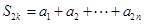
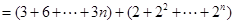
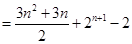
本题主要考查等差、等比数列的基本知识,考查运算及推理能力.对于此类问题要认真审题、冷静解析,加上扎实的基本功就可以解决问题.
(Ⅰ)首先因式分解求得方程的两根,由条件a2k-1≤a2k写出当k=1,2,3,4时相邻两项,
(Ⅱ)由(1),寻找规律,得到数列{an}中的相邻两项a2k-1、a2k的通项,最后采用分组求和的方法求数列{an}的前2n项和S2n
(I)解:方程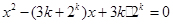 的两个根为
的两个根为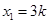 ,
,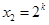 .
.
当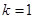 时,
时,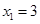 ,
,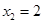 ,所以
,所以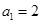 ;当
;当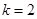 时,
时,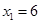 ,
,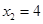 ,所以
,所以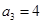 ;
;
当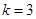 时,
时, ,
,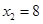 ,所以
,所以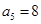 ;当
;当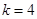 时,
时,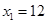 ,
,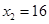 ,所以
,所以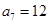 .
.
因为当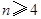 时,
时,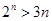 ,所以
,所以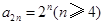 .
.
(II)解: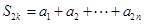
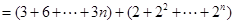
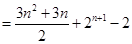
(Ⅰ)首先因式分解求得方程的两根,由条件a2k-1≤a2k写出当k=1,2,3,4时相邻两项,
(Ⅱ)由(1),寻找规律,得到数列{an}中的相邻两项a2k-1、a2k的通项,最后采用分组求和的方法求数列{an}的前2n项和S2n
(I)解:方程
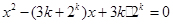 的两个根为
的两个根为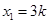 ,
,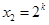 .
.当
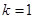 时,
时,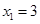 ,
,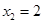 ,所以
,所以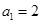 ;当
;当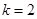 时,
时,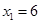 ,
,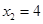 ,所以
,所以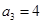 ;
;当
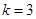 时,
时, ,
,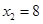 ,所以
,所以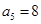 ;当
;当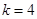 时,
时,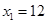 ,
,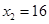 ,所以
,所以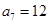 .
.因为当
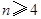 时,
时,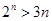 ,所以
,所以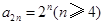 .
.(II)解:
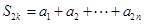
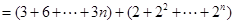
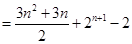

练习册系列答案
相关题目
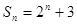 ,则
,则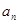 =_________.
=_________. ,如果
,如果 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数 性质”.不论数列
性质”.不论数列 ,且
,且 是
是 的一个排列;②数列
的一个排列;②数列 项和
项和 ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“ 的所有项按照从大到小,左大右小的原则写成如图所示的数表,第
的所有项按照从大到小,左大右小的原则写成如图所示的数表,第 行有
行有 个数,第
个数,第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则 可记为_________.
可记为_________.
 ,
, ,
, ,
, ,…,则
,…,则 是这个数列的
是这个数列的  满足
满足 ,则
,则 = ( )
= ( )
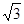

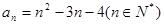 ,则a4等于( ).
,则a4等于( ).