题目内容
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】
(1)先求得A,B两点坐标,利用计算![]() 的周长可得p,进而求得抛物线方程;
的周长可得p,进而求得抛物线方程;
(2)利用导数的几何意义求得切线![]() 与
与![]() 的方程,联立直线与抛物线方程,利用韦达定理及
的方程,联立直线与抛物线方程,利用韦达定理及![]() 与
与![]() 的交点P,可得
的交点P,可得![]() ,再利用焦半径公式求得
,再利用焦半径公式求得![]() ,可得结果.
,可得结果.
(1)由题意知焦点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线
代入抛物线![]() 的方程可求得点
的方程可求得点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
有![]() ,
,![]() ,可得
,可得![]() 的周长为
的周长为![]() ,有
,有![]() ,得
,得![]() .
.
故抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)知抛物线![]() 的方程可化为
的方程可化为![]() ,求导可得
,求导可得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() .
.
设直线![]() 的方程为
的方程为![]() (直线
(直线![]() 的斜率显然存在).
的斜率显然存在).
联立方程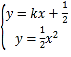 消去
消去![]() 整理为:
整理为:![]() ,可得
,可得![]() .
.
有![]() ,
,![]() .
.
可得直线![]() 的方程为
的方程为![]() ,整理为
,整理为![]() .
.
同理直线![]() 的方程为
的方程为![]() .
.
联立方程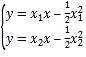 ,解得
,解得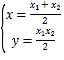 ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由抛物线的几何性质知![]() ,
,![]() ,
,
![]() .
.
有![]()
![]() .
.
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |

