题目内容
在下列五个函数中，①y=2x，②y=log2x，③y=x2，④y=x-1，⑤y=cos2x．当0＜x1＜x2＜1
时，使f(
)＞
恒成立的函数是______（将正确序号都填上）．
时，使f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∵f(
)＞
；表示连接两点A（x1，f（x1）），B （x2，f（x2））的线段的中点纵坐标小于f（x）在曲线AB中点 (
，f(
))；的纵坐标，
也就是说f（x）的图象“上凸”．所以只需判断哪个函数的图象“上凸”即可．
由图形可直观得到：①③④⑤的图象都不是上凸的，只有②为“上凸”的函数．
故答案为：②．
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
也就是说f（x）的图象“上凸”．所以只需判断哪个函数的图象“上凸”即可．
由图形可直观得到：①③④⑤的图象都不是上凸的，只有②为“上凸”的函数．
故答案为：②．
练习册系列答案
相关题目
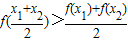恒成立的函数是 （将正确序号都填上）．
恒成立的函数是 （将正确序号都填上）．
恒成立的函数是 （将正确序号都填上）．