题目内容
设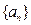 是公比大于1的等比数列,
是公比大于1的等比数列,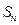 为数列
为数列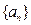 的前
的前 项和.已知
项和.已知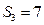 ,且
,且
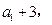
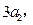
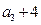 构成
构成 等差数列.
等差数列.
⑴求数列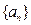 的通项;
的通项;
⑵令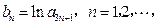 求数列
求数列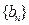 的前
的前 项和
项和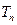 .
.

解析

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
题目内容
设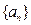 是公比大于1的等比数列,
是公比大于1的等比数列,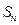 为数列
为数列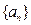 的前
的前 项和.已知
项和.已知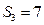 ,且
,且
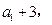
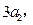
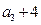 构成
构成 等差数列.
等差数列.
⑴求数列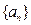 的通项;
的通项;
⑵令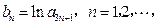 求数列
求数列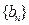 的前
的前 项和
项和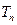 .
.

解析

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案