题目内容
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.(Ⅰ)求证:EF⊥B1C;
(Ⅱ)求三棱锥B1-EFC的体积.
分析:(Ⅰ)法一:由题意,欲证线线垂直,可先证出B1C⊥平面BC1D1再由线面垂直的性质证明EF⊥B1C即可;
法二:可由题设条件证明出EF⊥平面B1FC,再由线面垂直的性质得出线线垂直;
(Ⅱ)由题意,可先证明出CF⊥平面BDD1B1,由此得出三棱锥的高,再求出底面△B1EF的面积,然后再由棱锥的体积公式即可求得体积.
法二:可由题设条件证明出EF⊥平面B1FC,再由线面垂直的性质得出线线垂直;
(Ⅱ)由题意,可先证明出CF⊥平面BDD1B1,由此得出三棱锥的高,再求出底面△B1EF的面积,然后再由棱锥的体积公式即可求得体积.
解答: (Ⅰ)证明一:连接BD1,BC1
(Ⅰ)证明一:连接BD1,BC1
∵E、F分别为DD1、BD的中点∴EF∥BD1
∵正方体ABCD-A1B1C1D1
∴D1C1⊥平面BCC1B1∴D1C1⊥B1C
∵正方形BCC1B1∴B1C⊥BC1
∵D1C1∩BC1=C1∴B1C⊥平面BC1D1∴B1C⊥BD1
∵EF∥BD1∴EF⊥B1C
证明二:∵
=
=
=
∴Rt△EDF∽Rt△FBB1
∴∠DEF=∠BFB1∴∠BFB1+∠DFE=∠DEF+∠DFE=90°∴∠EFB1=90°
∴EF⊥FB1 又∵CF⊥平面BDD1B∴CF⊥EF
B1F∩CF=F∴EF⊥平面B1FC∴EF⊥B1C
(Ⅱ)∵CB=CD,BF=DF∴CF⊥BD∵DD1⊥平面ABCD∴DD1⊥CF
又DD1∩BD=D∴CF⊥平面BDD1B1 又CF=
方法一:△B1EF的面积=2×2
-
-
-
=
方法二: ∵EF⊥平面B1FC∴EF⊥FB1
∵EF⊥平面B1FC∴EF⊥FB1
EF=
,FB1=
Rt△B1EF的面积=
×EF×FB1=
×
×
=
∴VB1-EFC=VC-B1EF=
×S△B1EF×CF=
×
×
=1
∴三棱锥B1-EFC的体积为1.
 (Ⅰ)证明一:连接BD1,BC1
(Ⅰ)证明一:连接BD1,BC1∵E、F分别为DD1、BD的中点∴EF∥BD1
∵正方体ABCD-A1B1C1D1
∴D1C1⊥平面BCC1B1∴D1C1⊥B1C
∵正方形BCC1B1∴B1C⊥BC1
∵D1C1∩BC1=C1∴B1C⊥平面BC1D1∴B1C⊥BD1
∵EF∥BD1∴EF⊥B1C
证明二:∵
| ED |
| FB |
| 1 | ||
|
| ||
| 2 |
| DF |
| BB1 |
∴∠DEF=∠BFB1∴∠BFB1+∠DFE=∠DEF+∠DFE=90°∴∠EFB1=90°
∴EF⊥FB1 又∵CF⊥平面BDD1B∴CF⊥EF
B1F∩CF=F∴EF⊥平面B1FC∴EF⊥B1C
(Ⅱ)∵CB=CD,BF=DF∴CF⊥BD∵DD1⊥平面ABCD∴DD1⊥CF
又DD1∩BD=D∴CF⊥平面BDD1B1 又CF=
| 2 |
方法一:△B1EF的面积=2×2
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
方法二:
 ∵EF⊥平面B1FC∴EF⊥FB1
∵EF⊥平面B1FC∴EF⊥FB1EF=
| 3 |
| 6 |
Rt△B1EF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 6 |
| 3 |
| 2 |
| 2 |
∴VB1-EFC=VC-B1EF=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 2 |
| 2 |
∴三棱锥B1-EFC的体积为1.
点评:本题考查线面垂直的性质定理与线面垂直的判定定理及锥体的体积的求法,考查了空间感知能力及判断推理的能力,解题的关键是熟练掌握相关的定理及公式,本题是立体几何中的常规题题型,难度不大,计算麻烦.

练习册系列答案
相关题目
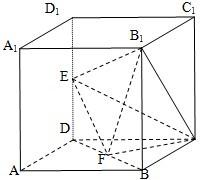 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.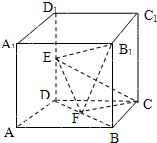 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点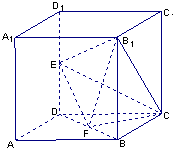 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 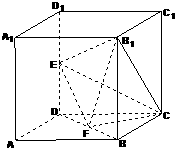 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.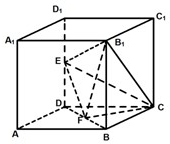 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.