题目内容
经过两点P1(
,
),P2(0,
)的椭圆的标准方程 .
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n),把两点P1(
,
),P2(0,
)代入,能求出结果.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
解L:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n)
把两点P1(
,
),P2(0,
)代入,得:
,
解得m=5,n=4,
∴椭圆方程为5x2+4y2=1,即
+
=1.
故答案为:
+
=1.
把两点P1(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
|
解得m=5,n=4,
∴椭圆方程为5x2+4y2=1,即
| x2 | ||
|
| y2 | ||
|
故答案为:
| x2 | ||
|
| y2 | ||
|
点评:本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量
如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量
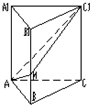 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=