题目内容
20.以坐标轴为对称轴,长、短半轴长之和为10,焦距为4$\sqrt{5}$的椭圆方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{16}=1$,或$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{36}=1$.分析 根据已知结合椭圆的简单性质,可得$\left\{\begin{array}{l}a+b=10\\{a}^{2}-{b}^{2}=(\frac{4\sqrt{5}}{2})^{2}\end{array}\right.$,解出a,b的值,可得答案.
解答 解:由已知可得:$\left\{\begin{array}{l}a+b=10\\{a}^{2}-{b}^{2}=(\frac{4\sqrt{5}}{2})^{2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=6\\ b=4\end{array}\right.$,
故椭圆的方程为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{16}=1$,或$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{36}=1$,
故答案为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{16}=1$,或$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{36}=1$
点评 本题考查的知识点是椭圆的标准方程,要注意由于没有说明焦点的位置,故要分两种情况.

练习册系列答案
相关题目
15.△ABC中,a,b,c分别是角A,B,C的对边,且sinA+cosA=$\frac{\sqrt{3}-1}{2}$,a=7,3sinB=5sinC,则b+c的值为( )
| A. | 12 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 8 |
12.已知等比数列{an}中,a4a8=9,则a3+a9的取值范围为( )
| A. | [6,+∞) | B. | [6,+∞)∪(-∞,-6] | C. | (6,+∞) | D. | (-6,6) |
1.已知函数f(x)=logsinβ(x2+ax+3)在区间(-∞,1)上递增,则实数a的取值范围是( )
| A. | (-4,-2] | B. | [-4,-2] | C. | (-4,+∞) | D. | (-∞,-2) |
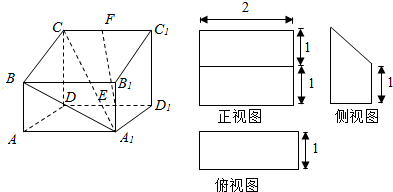 四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.
四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.