题目内容
如图,已知四边形ABCD内接于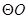 ,且AB是的
,且AB是的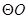 直径,过点D的
直径,过点D的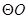 的切线与BA的延长线交于点M.
的切线与BA的延长线交于点M.
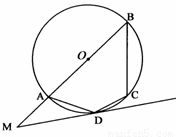
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小.
【答案】
(1)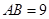 ;(2)
;(2)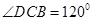 .
.
【解析】
试题分析:本题主要以圆为几何背景考查角的关系和边的关系,可以运用切割线定理、弦切角定理等数学知识来证明.第一问,先利用切割线定理得到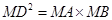 ,将已知条件代入,得到
,将已知条件代入,得到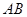 的长;第二问,因为
的长;第二问,因为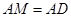 ,所以
,所以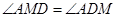 ,由弦切角定理得
,由弦切角定理得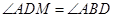 ,因为
,因为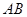 为直径,所以
为直径,所以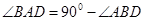 ,而
,而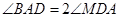 ,所以
,所以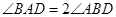 ,所以
,所以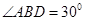 ,所以
,所以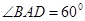 ,由于
,由于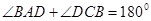 ,所以
,所以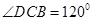 .
.
试题解析:(1)因为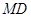 为
为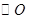 的切线,由切割线定理知,
的切线,由切割线定理知,
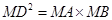 ,又
,又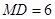 ,
,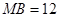 ,
,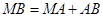 ,
,
所以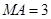 ,
,
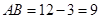 . 5分
. 5分
(2)因为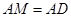 ,所以
,所以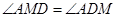 ,连接
,连接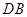 ,又
,又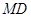 为
为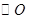 的切线,
的切线,
由弦切角定理知, 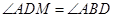 , 7分
, 7分
又因为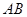 是
是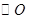 的直径,所以
的直径,所以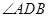 为直角,即
为直角,即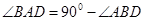 .
.
又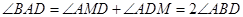 ,于是
,于是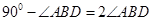 ,所以
,所以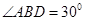 ,
,
所以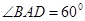 . 8分
. 8分
又四边形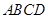 是圆内接四边形,所以
是圆内接四边形,所以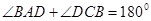 ,
,
所以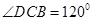 10分
10分
考点:1.切割线定理;2.弦切角定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. (几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切
(几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切 如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点
如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. 如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.
如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.