题目内容
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
[解析] 解法一:设光线l所在直线的方程为y-3=k(x+3),则反射点的坐标为![]() (k存在且k≠0).∵光线的入射角等于反射角,
(k存在且k≠0).∵光线的入射角等于反射角,
∴反射线l′所在直线的方程为
y=-k![]() ,即l′:y+kx+3(1+k)=0.
,即l′:y+kx+3(1+k)=0.
∵圆(x-2)2+(y-2)2=1与l′相切,
∴圆心到l′的距离d=![]() =1,
=1,
∴k=-![]() 或k=-
或k=-![]() ,
,
∴光线l所在直线的方程为3x+4y-3=0或4x+3y+3=0.
解法二:已知圆(x-2)2+(y-2)2=1关于x轴的对称圆C′的方程为(x-2)2+(y+2)2=1,如图所示.

可设光线l所在直线方程为y-3=k(x+3),
∵直线l与圆C′相切,
∴圆心C′(2,-2)到直线l的距离
d=![]() =1.解得k=-
=1.解得k=-![]() 或k=-
或k=-![]() .
.
∴光线l所在直线的方程为3x+4y-3=0或4x+3y+3=0.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
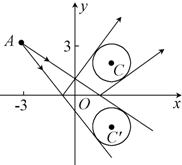 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
