题目内容
已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
解:(Ⅰ)因为椭圆![]() 上一点和它的两个焦点构成的三角形周长为
上一点和它的两个焦点构成的三角形周长为![]() ,
,
所以![]() , ……………1分
, ……………1分
又椭圆的离心率为![]() ,即
,即![]() ,所以
,所以![]() , ………………2分
, ………………2分
所以![]() ,
,![]() . ………………4分
. ………………4分
所以![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() . ………………5分
. ………………5分
(Ⅱ)方法一:不妨设![]() 的方程
的方程![]() ,则
,则![]() 的方程为
的方程为![]() .
.
由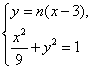 得
得![]() , ………………6分
, ………………6分
设![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() , …………7分
, …………7分
同理可得![]() , ………………8分
, ………………8分
所以![]() ,
,![]() , ………………10分
, ………………10分
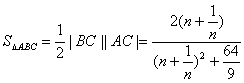 , ………………12分
, ………………12分
设![]() ,则
,则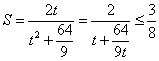 , ………………13分
, ………………13分
当且仅当![]() 时取等号,所以
时取等号,所以![]() 面积的最大值为
面积的最大值为![]() . ………………14分
. ………………14分
方法二:不妨设直线![]() 的方程
的方程![]() .
.
由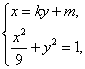 消去
消去![]() 得
得![]() , ………………6分
, ………………6分
设![]() ,
,![]() ,
,
则有![]() ,
,![]() . ① ………………7分
. ① ………………7分
因为以![]() 为直径的圆过点
为直径的圆过点![]() ,所以
,所以 ![]() .
.
由 ![]() ,
,
得 ![]() . ………………8分
. ………………8分
将![]() 代入上式,
代入上式,
得 ![]() .
.
将 ① 代入上式,解得 ![]() 或
或![]() (舍). ………………10分
(舍). ………………10分
所以![]() (此时直线
(此时直线![]() 经过定点
经过定点![]() ,与椭圆有两个交点),
,与椭圆有两个交点),
所以![]()
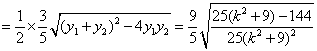 . ……………12分
. ……………12分
设![]() ,
,
则![]() .
.
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() . ……………14分
. ……………14分

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: