题目内容
判别下列函数的奇偶性:
①f(x)=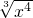 ________;②f(x)=
________;②f(x)=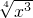 ________;③f(x)=
________;③f(x)=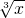 +
+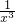 ________;④f(x)=|x+1|+|x-1|________;
________;④f(x)=|x+1|+|x-1|________;
⑤f(x)= ________;⑥f(x)=x+
________;⑥f(x)=x+ ________;
________;
偶函娄 非奇非偶函数 奇函数 偶函数 偶函数 奇函数
分析:由奇偶性定义判断,一是看定义域是否关于原点对称,二是看是否满足f(-x)与f(x)相等,还是互为相反数.
解答:①定义域R,且f(-x)=f(x)是偶函数
②定义域[,+∞)不关于原点对称,非奇非偶
③定义域为{x|x≠0}且f(-x)=-f(x)j是奇函数.
④定义域R,且f(-x)=f(x)是偶函数
⑤定义域是{x|x≠0}且f(-x)=f(x)是偶函数.
⑥定义域为{x|x≠0}且f(-x)=-f(x)
点评:本题主要考查如何应用奇偶性定义,要从两个方面:一是看定义域是否关于原点对称,二是看是否满足f(-x)与f(x)相等,还是互为相反数.
分析:由奇偶性定义判断,一是看定义域是否关于原点对称,二是看是否满足f(-x)与f(x)相等,还是互为相反数.
解答:①定义域R,且f(-x)=f(x)是偶函数
②定义域[,+∞)不关于原点对称,非奇非偶
③定义域为{x|x≠0}且f(-x)=-f(x)j是奇函数.
④定义域R,且f(-x)=f(x)是偶函数
⑤定义域是{x|x≠0}且f(-x)=f(x)是偶函数.
⑥定义域为{x|x≠0}且f(-x)=-f(x)
点评:本题主要考查如何应用奇偶性定义,要从两个方面:一是看定义域是否关于原点对称,二是看是否满足f(-x)与f(x)相等,还是互为相反数.

练习册系列答案
相关题目
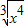 ;②f(x)=
;②f(x)=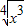 ;③f(x)=
;③f(x)=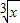 +
+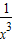 ;④f(x)=|x+1|+|x-1| ;
;④f(x)=|x+1|+|x-1| ;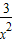 ;⑥f(x)=x+
;⑥f(x)=x+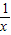 ;
;