题目内容
(本小题满分12分)在数列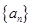 中,
中, 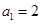 ,
,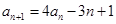 ,
,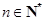 .
.
(Ⅰ)证明数列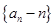 是等比数列;
是等比数列;
(II)求数列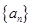 的前
的前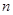 项和
项和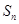 .
.
(Ⅲ)证明对任意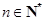 ,不等式
,不等式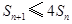 成立.
成立.
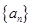 中,
中, 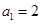 ,
,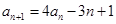 ,
,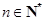 .
.(Ⅰ)证明数列
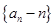 是等比数列;
是等比数列;(II)求数列
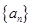 的前
的前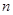 项和
项和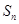 .
.(Ⅲ)证明对任意
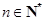 ,不等式
,不等式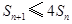 成立.
成立.(Ⅰ)由题设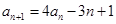 ,得
,得 ,
,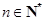 .
.
又 ,所以数列
,所以数列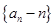 是首项为
是首项为 ,且公比为
,且公比为 的等比数列.
的等比数列.
(II) ;(Ⅲ)对任意的
;(Ⅲ)对任意的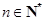 ,
,

 .
.
所以不等式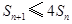 ,对任意
,对任意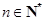 皆成立.
皆成立.
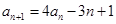 ,得
,得 ,
,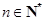 .
.又
 ,所以数列
,所以数列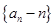 是首项为
是首项为 ,且公比为
,且公比为 的等比数列.
的等比数列.(II)
 ;(Ⅲ)对任意的
;(Ⅲ)对任意的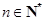 ,
,
 .
.所以不等式
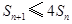 ,对任意
,对任意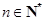 皆成立.
皆成立.试题分析:(Ⅰ)证明:由题设
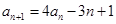 ,得
,得 ,
,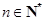 .
.又
 ,所以数列
,所以数列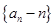 是首项为
是首项为 ,且公比为
,且公比为 的等比数列.…………4分
的等比数列.…………4分(Ⅱ)解:由(Ⅰ)可知
 ,于是数列
,于是数列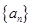 的通项公式为
的通项公式为 .
.所以数列
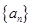 的前
的前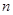 项和
项和 .…………8分
.…………8分(Ⅲ)证明:对任意的
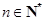 ,
,
 .
.所以不等式
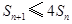 ,对任意
,对任意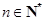 皆成立.…………12分
皆成立.…………12分点评:设数列
 ,其中
,其中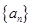 为等差数列,
为等差数列, 为等比数列,若求数列
为等比数列,若求数列 的前n项和,我们一般用分组求和法。分组求和法经常考到,我们要熟练掌握。
的前n项和,我们一般用分组求和法。分组求和法经常考到,我们要熟练掌握。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
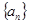 为单调递增的等差数列
为单调递增的等差数列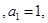 且
且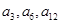 依次成等比数列.
依次成等比数列.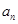 ;
;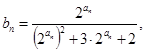 求数列
求数列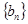 的前
的前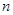 项和
项和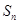 ;
;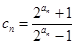 ,求证:
,求证: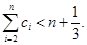
 满足:
满足: ,
, .
. .
. 及
及 ;
; ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
 中,
中, ,若
,若 ,则数列
,则数列 的前5项和等于 .
的前5项和等于 . 中,
中, ,若数列
,若数列 的前
的前 项和为
项和为 ,则
,则 前
前 项和为
项和为 ,
, .
. 为等比数列;
为等比数列; ,数列
,数列 前
前 ,求证:
,求证: .
. 是数列
是数列 的前
的前 项和,向量
项和,向量 ,
, ,且满足
,且满足 ,则
,则