题目内容
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1) 设动点P的坐标为![]() , 由题意可得
, 由题意可得![]() ,整理可得曲线E的方程;
,整理可得曲线E的方程;
(2) 解法一:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,分别与圆联立,可得
,分别与圆联立,可得![]() ,
,![]() ,可得
,可得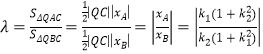 ,可得
,可得![]() ,代入可得答案;
,代入可得答案;
解法二:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]() ,
,![]()
![]() ,
,![]()
![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]() ,
,![]() ,可得
,可得![]() ,代入可得答案.
,代入可得答案.
解:(1)设动点P的坐标为![]() ,由题意可得
,由题意可得![]() ,
,
整理,得:![]() ,即
,即![]() 为所求曲线E的方程;
为所求曲线E的方程;
(2)(解法一)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以,![]()
同理,设直线NQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以![]()
因此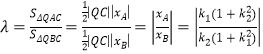
由于直线![]() 过坐标原点,所以点
过坐标原点,所以点![]() 与点
与点![]() 关于坐标原点对称
关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()
(解法二)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]()
所以![]()
于是,![]()
![]()
设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]()
所以![]()
由于直线l过坐标原点,所以点M与点N关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()

【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
(2)能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |