题目内容
在一个盒子里装有6张卡片，上面分别写着如下定义域为
的函数：
，
，
，
，
，
．
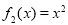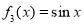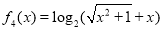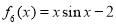（1）现在从盒子中任意取两张卡片，记事件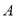
为“这两张卡片上函数相加，所得新函数是奇函数”，求事件
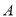的概率；
（2）从盒中不放回逐一抽取卡片，若取到一张卡片上的函数是偶函数则停止抽取，否则继续进行，记停止时抽取次数为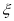
，写出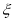
的分布列，并求其数学期望
．
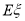练习册系列答案
名题金卷系列答案
相关题目
1．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，P为椭圆C上的一点，且位于第一象限，直线PO，PF分别交椭圆C于M，N两点．若△POF为正三角形，则直线MN的斜率等于（ ）
| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$-$\sqrt{2}$ | C． | 2-$\sqrt{2}$ | D． | 2-$\sqrt{3}$ |
18．已知数列{an}是递增的等比数列，a1+a4=9，a2a3=8，则数列{an}的前2016项之和S2016=（ ）
| A． | 22016 | B． | 22015-1 | C． | 22016-1 | D． | 22017-1 |
14．ABCD-A1B1C1D1是棱长为2的正方体，AC1、BD1相交于O，在正方体内（含正方体表面）随机取一点M，OM≤1的概率p=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{3}{π}$ | D． | $\frac{2}{π}$ |
18．下列函数既是奇函数，又在[-1，1]上单调递增是（ ）
| A． | f（x）=|sinx| | B． | f（x）=ln$\frac{2-x}{2+x}$ | C． | f（x）=$\frac{1}{2}$（ex-e-x） | D． | f（x）=ln（$\sqrt{{x}^{2}+1}$-x） |