题目内容
（2013•青岛二模）无限循环小数可以化为分数，如0.
=
，0.
=
，0.
1
=
…，请你归纳出0.
99
=
．
| • |
| 1 |
| 1 |
| 9 |
| • |
| 1 |
| • |
| 3 |
| 13 |
| 99 |
| • |
| 0 |
| • |
| 5 |
| 5 |
| 333 |
| • |
| 1 |
| • |
| 9 |
| 1999 |
| 9999 |
| 1999 |
| 9999 |
分析：通过分析给出的三个无限循环小数和分数的互化，看出有几位循环节分母就是含几个9的数字，而分子是小数点后从第一个非0数字开始的数，由此可归纳得到0.
99
化成的分数．
| • |
| 1 |
| • |
| 9 |
解答：解：由0.
=
，0.
=
，0.
1
=
=
，可以看出，无限循环小数在化分数时，得到的分数的分母的各个位置上的数字都是9，且循环节占几位就有几个9，而分子就是小数点后的数，首位从非零数字开始计数．
由此可以判断0.
99
=
．
故答案为
．
| • |
| 1 |
| 1 |
| 9 |
| • |
| 1 |
| • |
| 3 |
| 13 |
| 99 |
| • |
| 0 |
| • |
| 5 |
| 5 |
| 333 |
| 15 |
| 999 |
由此可以判断0.
| • |
| 1 |
| • |
| 9 |
| 1999 |
| 9999 |
故答案为
| 1999 |
| 9999 |
点评：本题考查了类比推理，类比推理是经过分析、观察、比较、联想，再进行归纳，类比，然后提出猜想的推理，此题是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013•青岛二模）一同学为研究函数f（x）=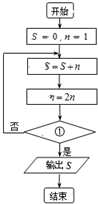
（2013•青岛二模）执行如图所示的程序框图．若输出S=31，则框图中①处可以填入（ ）