题目内容

过点P（2，3）做圆C：（x-1）2+（y-1）2=1的切线，设T为切点，则切线长|PT|=（　　）
分析：由圆的标准方程知圆心和半径，求出点P到圆心的距离，即可求出切线长．
解答：解：∵圆C：（x-1）2+（y-1）2=1，
∴圆心C为（1，1），半径r=1；
∴点P到圆心的距离为|PC|，则|PC|2=（2-1）2+（3-1）2=5，
∵圆的切线垂直于过切点的直径，
∴切线长|PT|=
|PC|2-r2
=
5-1
=2．
故选：D．
点评：本题考查了圆的标准方程以及两点间的距离公式的应用问题，是中档题．
练习册系列答案
相关题目
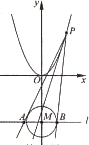精英家教网选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（1）若M，N分别是曲线ρ=2cosθ和ρsin(θ-
π
4
)=
2
2
上的动点，则M，N两点间的距离的最小值是
 
；
（2）不等式|2x-1|-x＜1的解集是
 
；
（3）如图，过点P作圆O的割线PAB与切线PE，E为切点，连接AE，BE，∠APE的平分线与AE，BE分别交于点C，D，若∠AEB=30°，则∠PCE=
 
°；
精英家教网如图，设P是抛物线C1：x2=y上的动点．过点P做圆C2：x2+（y+3）2=1的两条切线，交直线l：y=-3于A，B两点．
（Ⅰ）求C2的圆心M到抛物线 C1准线的距离．
（Ⅱ）是否存在点P，使线段AB被抛物线C1在点P处的切线平分？若存在，求出点P的坐标；若不存在，请说明理由．
【选做题】在A，B，C，D四小题中只能选做2题，每题10分，共计20分．请在答题卡指定区域内作答，解答时写出文字说明、证明过程或演算步骤．
21-1．（选修4-2：矩阵与变换）
设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
（1）求矩阵M的特征值及相应的特征向量；
（2）求逆矩阵M-1以及椭圆
x2
4
+
y2
9
=1在M-1的作用下的新曲线的方程．
21-2．（选修4-4：参数方程）
以直角坐标系的原点O为极点，x轴的正半轴为极轴．已知点P的直角坐标为（1，-5），点M的极坐标为（4，
π
2
），若直线l过点P，且倾斜角为 
π
3
，圆C以M为圆心、4为半径．
（1）求直线l关于t的参数方程和圆C的极坐标方程；
（2）试判定直线l和圆C的位置关系．
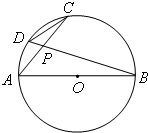（2007•深圳一模）请从下面两题中选做一题，如果两题都做，以第一题的得分为最后得分．
（1）在极坐标系中，过圆ρ=4cosθ的圆心，且垂直于极轴的直线方程为
ρcosθ=2
ρcosθ=2
．
（2）如图，AB为⊙O的直径，弦AC、BD交于点P，若AB=3，CD=1，则sin∠APD=
2
2
3
2
2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网