题目内容
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)(1)若M,N分别是曲线ρ=2cosθ和ρsin(θ-
| π |
| 4 |
| ||
| 2 |
(2)不等式|2x-1|-x<1的解集是
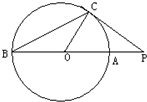
(3)如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=
分析:(1)可以先将极坐标方程化为直角坐标方程,M、N是直线与圆上的两个动点,最小距离为圆心到直线的距离减去半径即可;
(2)将绝对值不等式移项,两边平方,然后解一元二次不等式即可;
(3)利用弦切角,以及三角形的外角与内角的关系,结合图形即可解决.
(2)将绝对值不等式移项,两边平方,然后解一元二次不等式即可;
(3)利用弦切角,以及三角形的外角与内角的关系,结合图形即可解决.
解答:解:(1)曲线ρ=2cosθ和ρsin(θ-
)=
可化为直角坐标方程为:x-y+1=0与(x-1)2+y2=1
∴M、N在直线与圆心(1,0)半径为1的圆上
圆心(1,0)到直线的距离d=
=
∴M,N两点间的距离的最小值dmin=
-1 故答案为:
- 1
(2)|2x-1|-x<1
∴|2x-1|<x+1 两边平方得,
(2x-1)2<(x+1)2
∴x2-2x<0 即 0<x<2 故答案为(0,2)
(3)如图,PE 是圆的切线
∴∠PEB=∠PAC
∵AE是∠APE的平分线
∴∠EPC=∠APC
根据三角形的外角与内角关系有:∠EDC=∠PEB+∠EPC;∠ECD=∠PAC+∠APC
∴∠EDC=∠ECD
∴△EDC为等腰三角形,又∠AEB=30°
∴∠EDC=∠ECD=75°即∠PCE=75°,
故答案为75.
| π |
| 4 |
| ||
| 2 |
可化为直角坐标方程为:x-y+1=0与(x-1)2+y2=1
∴M、N在直线与圆心(1,0)半径为1的圆上
圆心(1,0)到直线的距离d=
| |2| | ||
|
| 2 |
∴M,N两点间的距离的最小值dmin=
| 2 |
| 2 |
(2)|2x-1|-x<1
∴|2x-1|<x+1 两边平方得,
(2x-1)2<(x+1)2
∴x2-2x<0 即 0<x<2 故答案为(0,2)

(3)如图,PE 是圆的切线
∴∠PEB=∠PAC
∵AE是∠APE的平分线
∴∠EPC=∠APC
根据三角形的外角与内角关系有:∠EDC=∠PEB+∠EPC;∠ECD=∠PAC+∠APC
∴∠EDC=∠ECD
∴△EDC为等腰三角形,又∠AEB=30°
∴∠EDC=∠ECD=75°即∠PCE=75°,
故答案为75.
点评:本题考查极坐标与直角坐标之间的转化,点到直线的距离,绝对值不等式的解法,以及圆与三角形相关知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)