题目内容
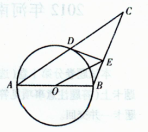
(几何证明选做题)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点 D,CD=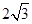 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 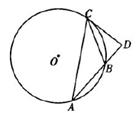
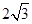 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 

解:∵CD是圆的切线,
∴∠BCD=∠A;
又∠D=∠D,
∴△BCD∽△CAD,
∴AC :BC =AD: CD ="CD" :BD ,
即AC :3 =3+BD: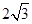 =
=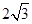 : BD ,
: BD ,
则BD=4或-7(负值舍去).
所以AC=
∴∠BCD=∠A;
又∠D=∠D,
∴△BCD∽△CAD,
∴AC :BC =AD: CD ="CD" :BD ,
即AC :3 =3+BD:
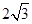 =
=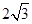 : BD ,
: BD ,则BD=4或-7(负值舍去).
所以AC=


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
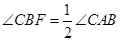 .
.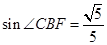 ,求BC和BF的长.
,求BC和BF的长.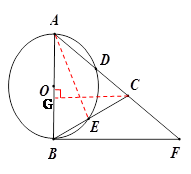
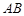 是⊙
是⊙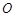 的一条切线,切点为
的一条切线,切点为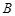 ,
,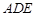 ,
,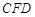 ,
,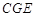 都是⊙
都是⊙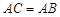 .
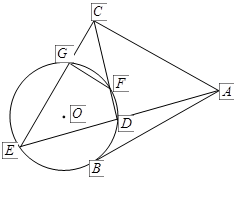
.
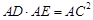 ;
; .
. ·
· 的值是
的值是 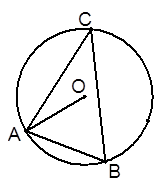
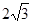 若
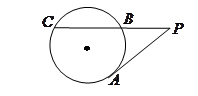
若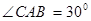 ,则圆O的直径AB等于( )
,则圆O的直径AB等于( )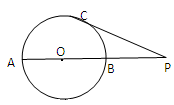 .
.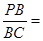
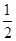 ,
,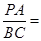
 1
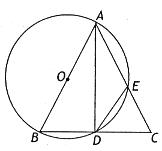
1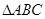 中,AB=BC,以AB为直径的⊙O交AC于点D,过D作
中,AB=BC,以AB为直径的⊙O交AC于点D,过D作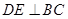 ,垂足为E,连结OE。若
,垂足为E,连结OE。若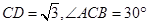 ,分别求AB,OE的长。
,分别求AB,OE的长。