题目内容
已知二阶矩阵M有特征值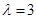 及对应的一个特征向量
及对应的一个特征向量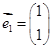 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点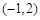 变换成
变换成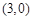 ,求矩阵M.
,求矩阵M.
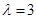 及对应的一个特征向量
及对应的一个特征向量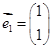 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点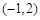 变换成
变换成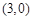 ,求矩阵M.
,求矩阵M.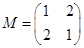 .
.试题分析:先设矩阵
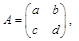 这里
这里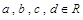 ,由二阶矩阵
,由二阶矩阵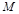 有特征值
有特征值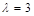 ,以及对应的一个特征向量
,以及对应的一个特征向量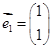 ,及矩阵
,及矩阵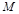 对应的变换将
对应的变换将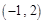 变换成
变换成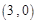 ,得到关于
,得到关于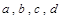 的方程组,即可求得矩阵
的方程组,即可求得矩阵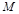 .
.试题解析:设矩阵
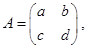 这里
这里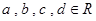 ,则
,则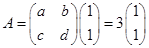 ,故
,故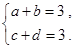
 ,故
,故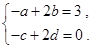 联立以上两方程组解得
联立以上两方程组解得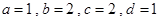 ,故
,故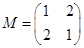 .
. 
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 及对应的一个特征向量
及对应的一个特征向量 ,且M
,且M =
= .求矩阵M.
.求矩阵M.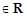 ,若
,若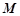 =
=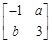 所对应的变换TM把直线2x-y=3变换成自身,试求实数a,b.
所对应的变换TM把直线2x-y=3变换成自身,试求实数a,b. ,
, ,求矩阵
,求矩阵
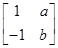 ,A的一个特征值λ=2,其对应的特征向量是α1=
,A的一个特征值λ=2,其对应的特征向量是α1=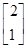 .设向量β=
.设向量β=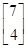 ,试计算A5β的值.
,试计算A5β的值.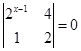 ,则
,则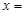 .
.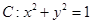 在矩阵
在矩阵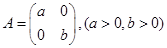 对应的变换下变成椭圆
对应的变换下变成椭圆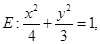 求矩阵
求矩阵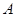 的逆矩阵
的逆矩阵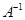 .
.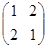 的特征值
的特征值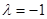 所对应的一个特征向量。
所对应的一个特征向量。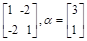 ,试计算
,试计算