题目内容
已知点O为△ABC的外心，且|| AC |
| AB |
| AO |
| BC |
分析：根据点O为△ABC的外心，且|
|=4，|
|=2，所以
•
=
•(
-
)=
•
-
•
=|
||
|cos＜AC，AO＞-|
||
|cos＜AB，AO＞
得到答案．
| AC |
| AB |
| AO |
| BC |
| AO |
| AC |
| AB |
| AO |
| AC |
| AO |
| AB |
=|
| AC |
| AO |
| AB |
| AO |
得到答案．
解答：解：∵点O为△ABC的外心，且|
|=4，|
|=2，
∴
•
=
•(
-
)=
•
-
•
=|
||
|cos＜AC，AO＞-|
||
|cos＜AB，AO＞
=|
||
|×
-|
||
|×
=
(4×4-2×2)=6
故答案为：6
| AC |
| AB |
∴
| AO |
| BC |
| AO |
| AC |
| AB |
| AO |
| AC |
| AO |
| AB |
=|
| AC |
| AO |
| AB |
| AO |
=|
| AC |
| AC |
| 1 |
| 2 |
| AB |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：6
点评：本题主要考查向量数量积的几何意义．要会巧妙的转化问题．属中档题．
练习册系列答案
相关题目
已知点O为△ABC的外心，且|
|=4，|
|=2则
•
=（ ）
| AC |
| AB |
| AO |
| BC |
| A、2 | ||
| B、4 | ||
C、2
| ||
| D、6 |
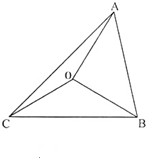（2011•杭州一模）已知点O为△ABC的外心，角A，B，C的对边分别满足a，b，c，
，
，则
的值等于 ．