题目内容
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E,F分别为棱BC,DC上的动点,且BE=CF.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E,F分别为棱BC,DC上的动点,且BE=CF.
(1)求证:B1F⊥D1E;
(2)当三棱锥C1-FCE的体积取到最大值时,求二面角C1-FE-C的正切值.
解:(1)如图,以D为坐标原点,直线DA、DC、DD1分别x轴、y轴、z轴,建立空间直角坐标系,
如图所示:
设BE=CF=b,
则D1(0,0,a),E(a-b,a,0),F(0,a-b,0),B1(a,a,a),
所以 ,
, ,
,
所以 ,
,
所以B1F⊥D1E.
(2)由题意可得:当三棱锥C1-FCE的体积取到最大值时,即其底面积△FEC最大,即S△FEC= b(a-b)最大,
b(a-b)最大,
由二次函数的性质可得:当b= 时,其底面积取最大值,即点E、F分别是
时,其底面积取最大值,即点E、F分别是
BC、CD的中点,
所以C1F=C1E,CE=CF.
取EF的中点为O,连接C1O,CO,
所以C1O⊥EF,CO⊥EF,
所以∠C1OC为二面角C1-FE-C的平面角.
在△C1OC中,C1C=a,CO=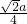 ,所以tan∠C1OC=2
,所以tan∠C1OC=2 .
.
所以二面角C1-FE-C的正切值为2 .
.
分析:(1)因为是正方体,又是空间垂直问题,所以易采用向量法,所以建立如图所示的空间直角坐标系D-xyz,欲证B1F⊥D1E,只须证 再用向量数量积公式求解即可.
再用向量数量积公式求解即可.
(2)由题意可得:当三棱锥C1-FCE的体积取到最大值时,即其底面积△FEC最大,可得点E、F分别是BC、CD的中点时取最大值,再根据线面关系得到∠C1OC为二面角C1-FE-C的平面角,进而利用解三角形的有关知识求出答案即可.
点评:本题主要考查向量证明线线的垂直关系,以及考查几何体的体积与二面角的平面角等问题,也可以利用向量的方法解决二面角的问题,次方法比较方便灵活,是常考类型,属中档题.
如图所示:

设BE=CF=b,
则D1(0,0,a),E(a-b,a,0),F(0,a-b,0),B1(a,a,a),
所以
 ,
, ,
,所以
 ,
,所以B1F⊥D1E.
(2)由题意可得:当三棱锥C1-FCE的体积取到最大值时,即其底面积△FEC最大,即S△FEC=
 b(a-b)最大,
b(a-b)最大,由二次函数的性质可得:当b=
 时,其底面积取最大值,即点E、F分别是
时,其底面积取最大值,即点E、F分别是BC、CD的中点,
所以C1F=C1E,CE=CF.
取EF的中点为O,连接C1O,CO,
所以C1O⊥EF,CO⊥EF,
所以∠C1OC为二面角C1-FE-C的平面角.
在△C1OC中,C1C=a,CO=
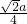 ,所以tan∠C1OC=2
,所以tan∠C1OC=2 .
.所以二面角C1-FE-C的正切值为2
 .
.分析:(1)因为是正方体,又是空间垂直问题,所以易采用向量法,所以建立如图所示的空间直角坐标系D-xyz,欲证B1F⊥D1E,只须证
 再用向量数量积公式求解即可.
再用向量数量积公式求解即可.(2)由题意可得:当三棱锥C1-FCE的体积取到最大值时,即其底面积△FEC最大,可得点E、F分别是BC、CD的中点时取最大值,再根据线面关系得到∠C1OC为二面角C1-FE-C的平面角,进而利用解三角形的有关知识求出答案即可.
点评:本题主要考查向量证明线线的垂直关系,以及考查几何体的体积与二面角的平面角等问题,也可以利用向量的方法解决二面角的问题,次方法比较方便灵活,是常考类型,属中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





